986. Interval List Intersections

置顶

Created At : 2023-10-28 15:14

Count:1k Views 👀 :

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval[a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

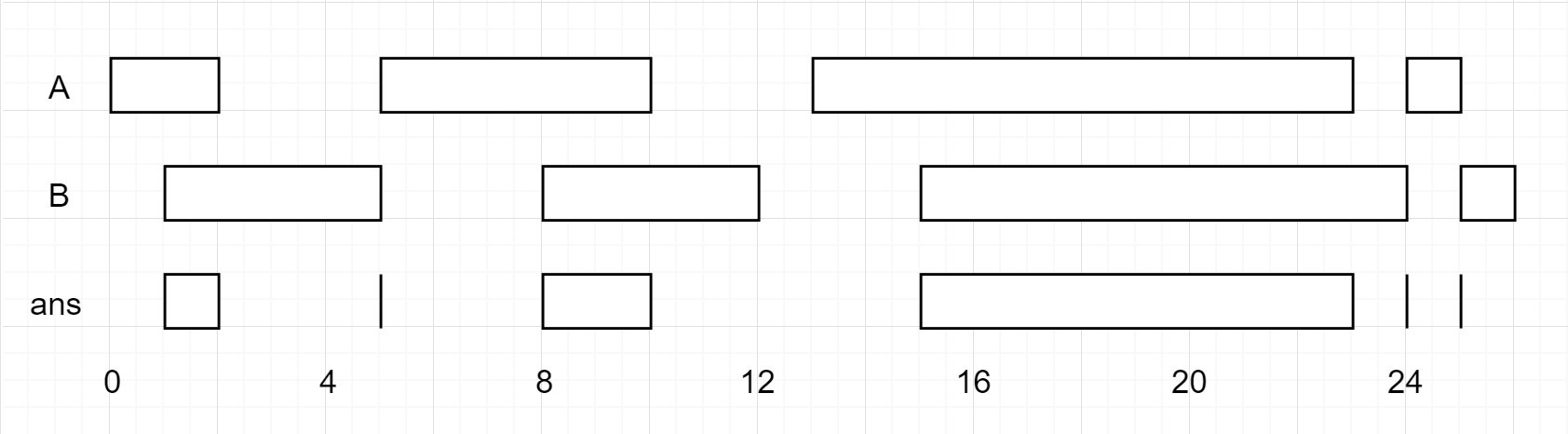
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Note:

0 <= A.length < 1000
0 <= B.length < 1000
0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

这道题给了两个区间数组，让返回所有相交的区间组成的数组。题目中的例子很贴心的还配了图，可以很直观的看出来相交的区间，而且可以注意到题目允许起始和结束位置相同的区间。这种类似合并区间的问题之前也做过 Merge Intervals，但是那道是只有一个区间数组进行合并，而这道题给了两个区间数组找相交区间，其实问题的本质都一样。对于这道题，由于求相交区间是要两两进行比较的，所以比较好的解法就是使用双指针来做，分别指向A和B中的某一个区间。这里用i和j两个变量表示，初始化为0，进行 while 循环，循环条件是i和j均没有遍历到末尾，然后来考虑，假如两个区间没有交集，就不用进行操作，直接平移指针即可。若i指向的区间在左边，即 A[i][1] < B[j][0] 时，i自增1，若j指向的区间在左边，即 B[j][1] < A[i][0] 时，j自增1，否则就是有交集，求交集的方法也简单，就是两个区间的起始位置中的较大值，和结束位置中的较小值组成的。将相交区间加入结果 res 后，还要平移指针，此时看，若i指向的区间结束位置小，则i自增1，若j指向的区间结束位置小，则j自增1，若二者相同，则i和j均自增1。这样循环退出后，所有的相交区间就保存在结果 res 中了，参见代码如下：

解法一：

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        int m = A.size(), n = B.size(), i = 0, j = 0;
        vector<vector<int>> res;
        while (i < m && j < n) {
            if (A[i][1] < B[j][0]) {
                ++i;
            } else if (B[j][1] < A[i][0]) {
                ++j;
            } else {
                res.push_back({max(A[i][0], B[j][0]), min(A[i][1], B[j][1])});
                if (A[i][1] < B[j][1]) ++i;
                else if (B[j][1] < A[i][1]) ++j;
                else {++i; ++j;}
            }
        }
        return res;
    }
};

我们也可以再写的简洁一些，其实并不用单独处理不相交的情况，只要分别求出两个区间起始位置的较大值，和结束位置的较小值，只要当前者小于等于后者时，相交区间才存在，此时才需要加入结果 res 中，然后还是根据两个区间结束位置的大小关系来平移指针，这样的写法就简洁多了，参见代码如下：

解法二：

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        int m = A.size(), n = B.size(), i = 0, j = 0;
        vector<vector<int>> res;
        while (i < m && j < n) {
            int lo = max(A[i][0], B[j][0]), hi = min(A[i][1], B[j][1]);
            if (lo <= hi) res.push_back({lo, hi});
            (A[i][1] < B[j][1]) ? ++i : ++j;
        }
        return res;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/986

类似题目：

Merge Intervals

Merge Sorted Array

Employee Free Time

参考资料：

https://leetcode.com/problems/interval-list-intersections/

https://leetcode.com/problems/interval-list-intersections/discuss/231108/C%2B%2B-O(n)-"merge-sort"

https://leetcode.com/problems/interval-list-intersections/discuss/646988/C%2B%2B-or-Easy-or-6-lines-or-Two-pointer-or-100

LeetCode All in One 题目讲解汇总(持续更新中…)

转载请注明来源于 Grandyang 的博客 (grandyang.com)，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 grandyang@qq.com