We have n chips, where the position of the ith chip is position[i].
We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:
position[i] + 2orposition[i] - 2withcost = 0.position[i] + 1orposition[i] - 1withcost = 1.
Return the minimum cost needed to move all the chips to the same position.
Example 1:
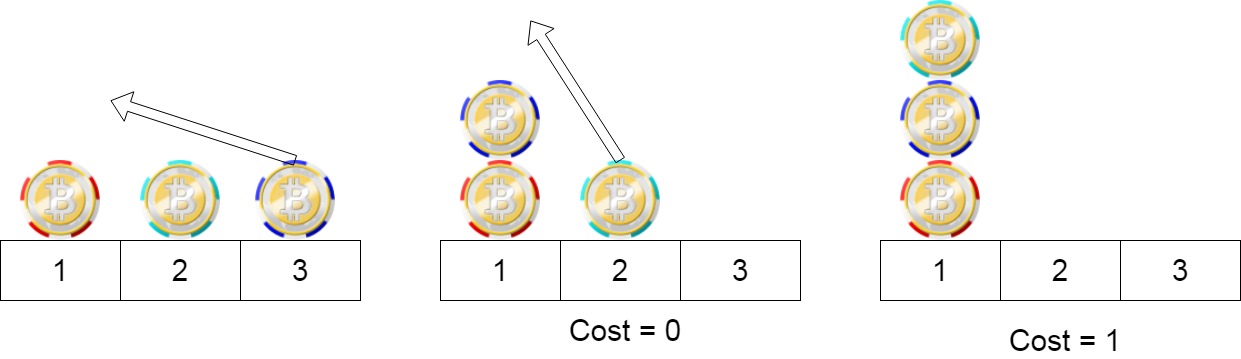
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.
Example 2:
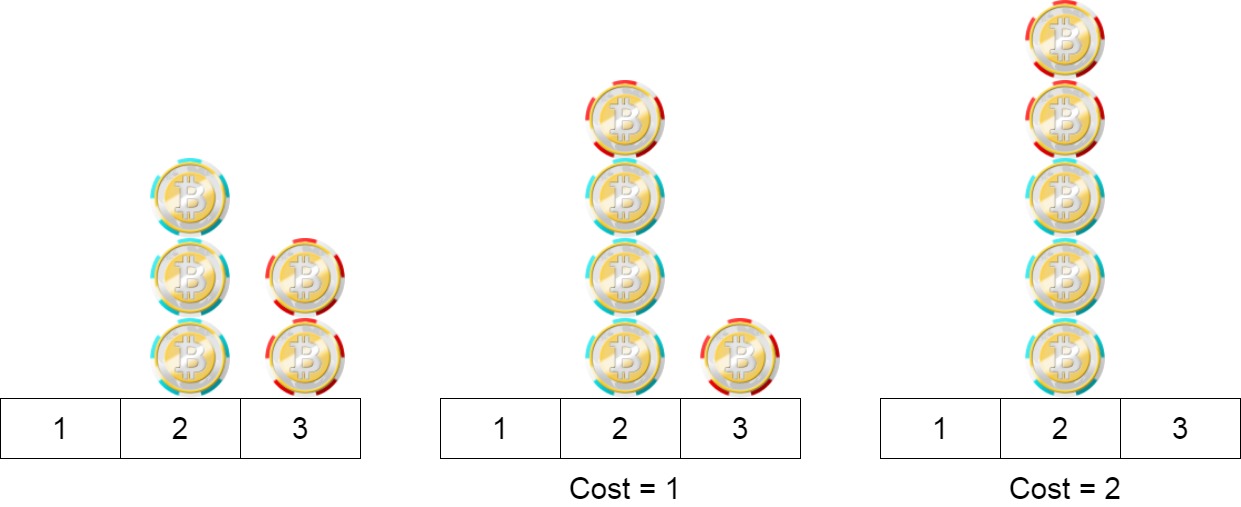
Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at position 3 to position 2. Each move has cost = 1. The total cost = 2.
Example 3:
Input: position = [1,1000000000]
Output: 1
Constraints:
1 <= position.length <= 1001 <= position[i] <= 10^9
这道题说是有一堆筹码,第i个筹码所在的位置是 position[i],现在需要将所有的筹码移动到一摞,规则是:左右移动两个位置没有 cost,左右移动一个位置需要花费1个 cost,问移动到同一摞需要的最少花费是多少。博主最先做的时候,一看既然是 Easy 题目,就别多想了,直接上暴力破解呗,找到 position 数组中的最大最小值,然后遍历每一个位置,都统计所有筹码移动到这个位置上的总花费,然后返回一个最小值,结果被 OJ 打脸,超时了 Time Limit Exceeded。直接过不去的就是题目中的例子3,这种方法要把范围中的十亿个位置都遍历一遍,能不超时么。所以博主想了下,最终合成一摞的位置肯定是在某一个已经存在的筹码的位置。
严谨的证明博主也不会,这里就大概说一下博主能想到的原因,若最终位置不在某个已经存在的筹码的位置,那么看该位置距离任意一个筹码的距离是否有偶数距离,有的话最终位置其实可以移动到那个筹码的位置,因为偶数距离之间的移动没有花费。若最终位置距离所有筹码的位置均为奇数(则所有筹码之间的距离均为偶数),那么该位置根本不应该成为最终位置,因为奇数距离都是有花费的。综上所述,最终结果位置必定在某一个已经存在的筹码的位置,那么这里其实就可以遍历所有给定筹码的位置,然后统计每个位置的花费。但其实这里还可以进一步优化,若有很多筹码都在同一个位置,那么显然按筹码遍历就不是很高效了,因为同一摞的筹码可以一起移动,则花费可以一起计算。这里用一个 HashMap 统计每个位置上的筹码个数,这样就可以把相同位置上的筹码摞到一起了。然后就可以遍历每一个位置了,对于遍历到的位置,再遍历其他所有的位置,统计花费,这样只要找到距离目标奇数位置,就可以把整个一摞的花费一起加上了。最后每次更新结果 res 即可,参见代码如下:
解法一:
class Solution {
public:
int minCostToMoveChips(vector<int>& position) {
int res = INT_MAX;
unordered_map<int, int> posCnt;
for (int pos : position) ++posCnt[pos];
for (auto &a : posCnt) {
int sum = 0;
for (auto &b : posCnt) {
if ((b.first - a.first) % 2 == 0) continue;
sum += b.second;
}
res = min(res, sum);
}
return res;
}
};
其实这道题还有更加简洁高效的解法,因为距离为偶数的筹码可以事先移动到一摞,而所有奇数位置的筹码互相之间都是相距偶数的距离,所有偶数位置的筹码互相之间也都是相距偶数的距离。这样所有筹码就可以在花费为0的情况下归为相邻的两大摞,则总花费其实就是个数较小的那一摞,参见代码如下:
解法二:
class Solution {
public:
int minCostToMoveChips(vector<int>& position) {
int even = 0, odd = 0;
for (int pos : position) {
(pos % 2 == 1) ? ++odd : ++even;
}
return min(odd, even);
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1217
类似题目:
Minimum Number of Operations to Move All Balls to Each Box
参考资料:
https://leetcode.com/problems/minimum-cost-to-move-chips-to-the-same-position/
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




