You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).
You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.
You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].
Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.
Example 1:
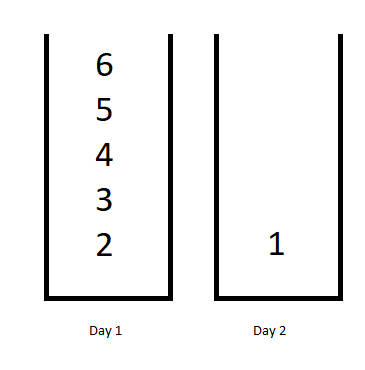
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7
Example 2:
Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
Example 3:
Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.
Constraints:
1 <= jobDifficulty.length <= 3000 <= jobDifficulty[i] <= 10001 <= d <= 10
这道题说是需要在d天内安排一些工作,且说明各项工作要按照顺序做,给定了每项工作的难度,放在数组 jobDifficulty 中。现在说是每天至少要完成一项工作,定义整个工作安排的难度为每天的难度之和,而每天的难度为当前最难的那项工作的难度,现在让返回d天的最小工作安排的难度。通过分析题目中给定的例子不难理解题意,其中例子2是一种 corner case,即若工作的个数小于天数的话是没法安排的,因为题目中限定了每天至少做一项工作。为了找出题目的本质考查点,需要褪去背景设定,这道题的本质就是要将给定的数组 jobDifficulty 分为d个子数组,然后将每个子数组中的最大值加起来,使得这个总和最小。看穿了本质之后,就要来考虑如何解题了,对于这种玩数组求极值的题目,基本上动态规划 Dynamic Programming 就是不二之选了。
首先来考虑下 DP 数组如何定义,这里的主要信息就是天数和工作数,可以用一个二维数组,其中 dp[i][j] 表示当前安排到第 ith 天(0开头的),且最后一个工作安排到第 jth 个工作,此时的最小难度。将 dp 数组初始化为整型最大值,将 dp[0][0] 初始化为0,因为此时安排到第0天,且唯一安排到的工作就是第0个工作(注意这里计数是从0开始的),则难度就是该工作的难度值 jobDifficulty[0]。接下来需要更新所有的 dp[0][j],因为当前只安排了一天工作,那么不论最后安排到哪个工作,都应该在一天内完成,则难度是 [0, j] 范围内的最大值。于是可以用 dp[0][j-1] 和 jobDifficulty[j] 中的较大值来更新 dp[0][j]。
接下来求状态转移方程,对于任意的 dp[i][j] 来说,此时安排到第 ith 天,且最后安排到的工作为第 jth 个,此时区间 [0, j] 内的工作都已经安排过了,对于今天做了多少工作我们不确定,但是可以遍历今天可以安排工作的所有情况,比如今天可能只安排了第 jth 个工作,那么今天的 dp 值就应该是 dp[i-1][j-1] + jobDifficulty[j] 了,因为前一天工作安排到第 j-1 个工作,加上工作j的难度就是今天 dp 值了。但是今天也可以安排多个工作,比如今天可以安排 [i, j] 中若干个工作(即从工作j开始往前直到工作i),不能安排第 ith 个工作之前第工作,因为要保证之前每天至少安排了一个工作,也不能大于第 jth 个工作,因为这是今天能安排到的最后一个工作。需要遍历所有的情况,同时找出该区间段的最大值 curMax,加到前一个 dp 值上,于是可以用 dp[i-1][k-1] + curMax 来更新 dp[i][j],最终的结果保存在 dp[d-1][n-1] 中返回即可,参见代码如下:
解法一:
class Solution {
public:
int minDifficulty(vector<int>& jobDifficulty, int d) {
int n = jobDifficulty.size();
if (d > n) return -1;
vector<vector<int>> dp(d, vector<int>(n, INT_MAX));
dp[0][0] = jobDifficulty[0];
for (int j = 1; j < n; ++j) {
dp[0][j] = max(dp[0][j - 1], jobDifficulty[j]);
}
for (int i = 1; i < d; ++i) {
for (int j = i; j < n; ++j) {
int curMax = jobDifficulty[j];
for (int k = j; k >= i; --k) {
curMax = max(curMax, jobDifficulty[k]);
dp[i][j] = min(dp[i][j], dp[i - 1][k - 1] + curMax);
}
}
}
return dp[d - 1][n - 1];
}
};
我们也可以使用递归加记忆数组的方式来做,这里为了递归方便,将 memo 数组大小定为 d+1 by n,均初始化为 -1。在递归函数中,首先是一系列的终止条件判断,若 dayLeft 为0了,且 idx 为n了,则返回0,表示此时没有工作需要安排,所以难度为0。否则若 dayLeft 为0,或者 idx 为0,说明此时状态不合法,不能成功的安排工作,返回整型最大值。否则若当前状态 memo[dayLeft][idx] 不为-1,说明当前状态之前计算过了,直接返回 memo 中的值即可。否则就要进行计算了,定义 curMax 为工作 idx 的难度,核心思想跟上面的 dp 方法基本相同,i从 idx 遍历到n,更新当前范围内的最大值 curMax,表示今天安排 [idx, i] 范围内的所有工作,然后调用递归函数,参数传入 dayLeft-1 和 i+1,判断若返回值不等于整型最大值 INT_MAX,说明可以成功安排,用其返回值更新最终结果 res,最后将当前状态 memo[dayLeft][idx] 赋值为 res 并返回即可,参见代码如下:
解法二:
class Solution {
public:
int minDifficulty(vector<int>& jobDifficulty, int d) {
int n = jobDifficulty.size();
if (d > n) return -1;
vector<vector<int>> memo(d + 1, vector<int>(n, -1));
return dfs(jobDifficulty, d, 0, memo);
}
int dfs(vector<int>& jobDifficulty, int dayLeft, int idx, vector<vector<int>>& memo) {
int n = jobDifficulty.size();
if (dayLeft == 0 && idx == n) return 0;
if (dayLeft == 0 || idx == n) return INT_MAX;
if (memo[dayLeft][idx] != -1) return memo[dayLeft][idx];
int curMax = jobDifficulty[idx], res = INT_MAX;
for (int i = idx; i < n; ++i) {
curMax = max(curMax, jobDifficulty[i]);
int t = dfs(jobDifficulty, dayLeft - 1, i + 1, memo);
if (t != INT_MAX) {
res = min(res, t + curMax);
}
}
return memo[dayLeft][idx] = res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1335
参考资料:
https://leetcode.com/problems/minimum-difficulty-of-a-job-schedule
LeetCode All in One 题目讲解汇总(持续更新中…)
(欢迎加入博主的知识星球,博主将及时答疑解惑,并分享刷题经验与总结,快快加入吧~)
微信打赏
 |
|
Venmo 打赏

—|—
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com





