There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.
Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities i and j is equal to the sum of the edges’ weights along that path.
Example 1:
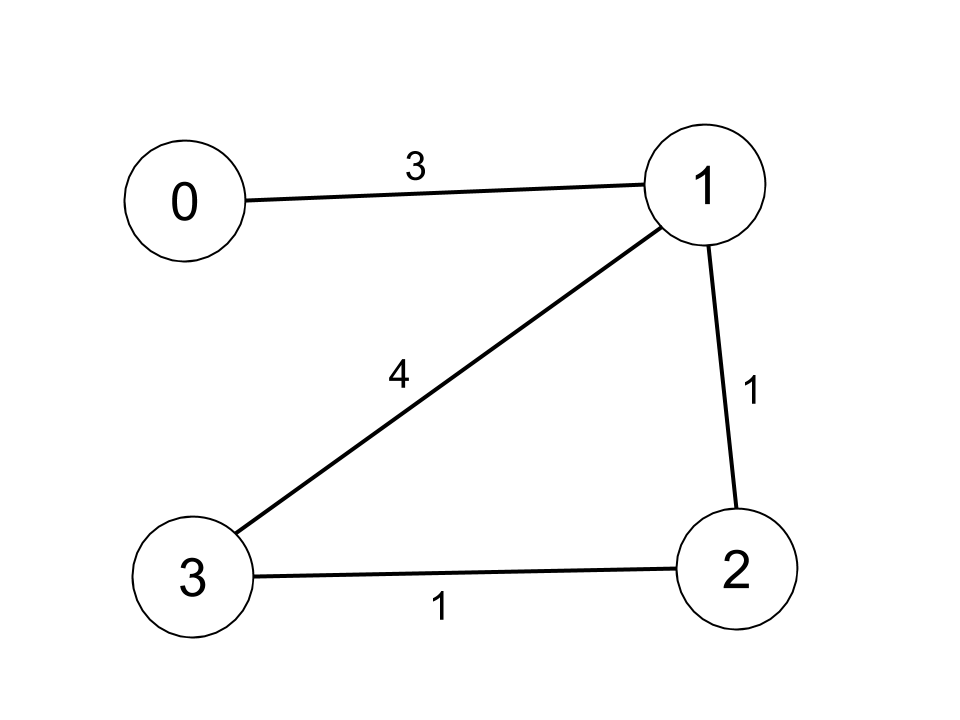
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph.
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2]
City 1 -> [City 0, City 2, City 3]
City 2 -> [City 0, City 1, City 3]
City 3 -> [City 1, City 2]
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
Example 2:
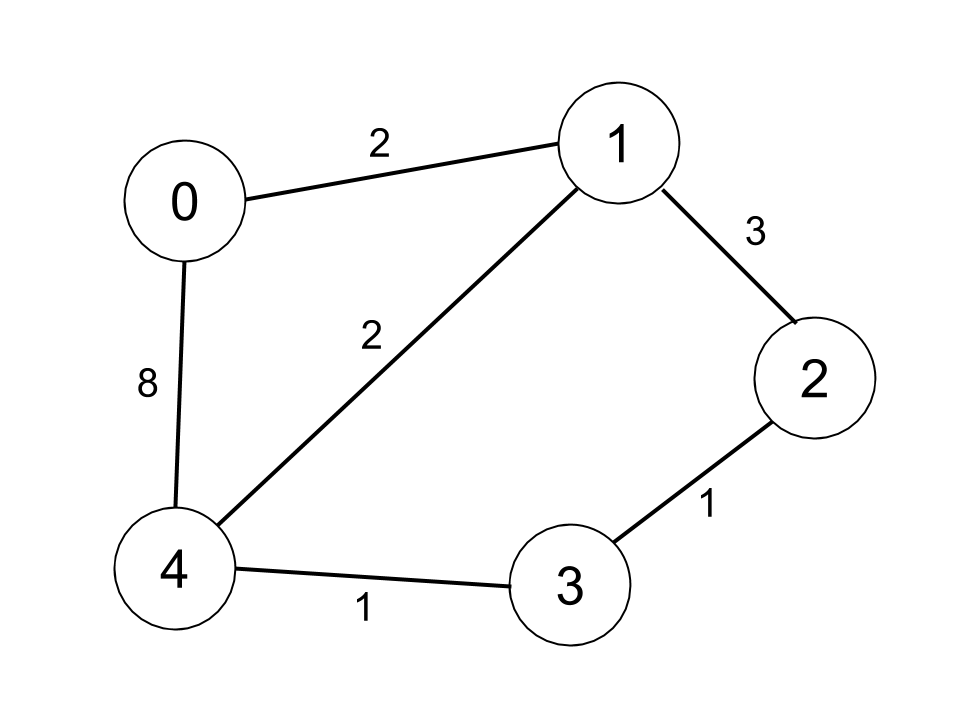
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph.
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1]
City 1 -> [City 0, City 4]
City 2 -> [City 3, City 4]
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3]
The city 0 has 1 neighboring city at a distanceThreshold = 2.
Constraints:
2 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= fromi < toi < n1 <= weighti, distanceThreshold <= 10^4- All pairs
(fromi, toi)are distinct.
这道题给了n个城市,还有一个 edges 数组,每条边包含了起始点,终止点,和距离。又给了一个变量 distanceThreshold,现在定义两个城市间的最短距离若小于给定的这个阈值的话,就表示这两个城市是连通的 reachable。现在让找到一个与其他城市相连通个数最少的城市,若出现相同个数,则返回城市编号最大的那个。这道题实际上是一道无向图的题目,其中n个城市就是图中的n个结点。因为两个城市的距离要小于给定的阈值,才表示是联通的,则需要求两个城市间的最短距离。求无向图中两点间的最小距离有很多方法,常用解法有迪杰斯特拉算法 Dijkstra Algorithm, 弗洛伊德算法 Floyd-Warshall Algorithm, 和贝尔曼福特算法 Bellman-Ford Algorithm,其中,Floyd 算法是多源最短路径,即求任意点到任意点到最短路径,而 Dijkstra 算法和 Bellman-Ford 算法是单源最短路径,即单个点到任意点到最短路径。这里明显要求任意两点之间的最小距离,于是乎 Floyd 算法就是不二之选了。
这里要先引入松弛操作 Relaxtion,这是这三个算法的核心思想,当有对边 (u, v) 是结点u到结点v,如果 dist(v) > dist(u) + w(u, v),那么 dist(v) 就可以被更新,这是所有这些的算法的核心操作。这里先定义上 dist 数组,其中 dist[i][j] 表示城市i到城市j之间的最小距离,初始化一个大值,但不要初始化为整型最大值,因为在之后的操作中可能会越界。这里初始化为 10^6 就可以了。然后要把所有 dist[i][i] 初始化为0,因为自己与自己之间没有距离。之后就需要用给定的 edges 数组来更新了,由于是无向图,同一个权重两个方向都要更新。然后就是 Floyd 算法的核心松弛操作了,这里需要用三个 for 循环嵌套,最外层的是k,中间依次是i和j,其中松弛操作的核心就是不停的用 dist[i][k] + dist[k][j] 来更新 dist[i][j]。更新完成之后,任意两个城市之间的最短距离就有了,接下来就是统计每个城市的连通城市个数,对于每个城市,遍历其他所有城市,若小于给定阈值,则计数器自增1,维护一个全局最小值,然后不停的更新这个全局最小值,同时记录下出现全局最小值时的城市编号即可,参见代码如下:
class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
int res = 0, minReachable = INT_MAX;
vector<vector<int>> dist(n, vector<int>(n, 1e6));
for (int i = 0; i < n; ++i) {
dist[i][i] = 0;
}
for (auto &edge : edges) {
dist[edge[0]][edge[1]] = edge[2];
dist[edge[1]][edge[0]] = edge[2];
}
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
for (int i = 0; i < n; ++i) {
int reachable = 0;
for (int j = 0; j < n; ++j) {
if (dist[i][j] <= distanceThreshold) ++reachable;
}
if (reachable <= minReachable) {
minReachable = reachable;
res = i;
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1334
类似题目:
Second Minimum Time to Reach Destination
参考资料:
LeetCode All in One 题目讲解汇总(持续更新中…)
(欢迎加入博主的知识星球,博主将及时答疑解惑,并分享刷题经验与总结,快快加入吧~)
微信打赏
 |
|
Venmo 打赏

—|—
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com





