510. Inorder Successor in BST II

置顶

Created At : 2023-10-28 15:14

Count:2k Views 👀 :

Given a binary search tree and a node in it, find the in-order successor of that node in the BST.

The successor of a node p is the node with the smallest key greater than p.val.

You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node.

Example 1:

Input: 
root = {"$id":"1","left":{"$id":"2","left":null,"parent":{"$ref":"1"},"right":null,"val":1},"parent":null,"right":{"$id":"3","left":null,"parent":{"$ref":"1"},"right":null,"val":3},"val":2}
p = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both p and the return value is of Node type.

Example 2:

Input: 
root = {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":{"$id":"4","left":null,"parent":{"$ref":"3"},"right":null,"val":1},"parent":{"$ref":"2"},"right":null,"val":2},"parent":{"$ref":"1"},"right":{"$id":"5","left":null,"parent":{"$ref":"2"},"right":null,"val":4},"val":3},"parent":null,"right":{"$id":"6","left":null,"parent":{"$ref":"1"},"right":null,"val":6},"val":5}
p = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Example 3:

Input: 
root = {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":{"$id":"4","left":null,"parent":{"$ref":"3"},"right":null,"val":2},"parent":{"$ref":"2"},"right":{"$id":"5","left":null,"parent":{"$ref":"3"},"right":null,"val":4},"val":3},"parent":{"$ref":"1"},"right":{"$id":"6","left":null,"parent":{"$ref":"2"},"right":{"$id":"7","left":{"$id":"8","left":null,"parent":{"$ref":"7"},"right":null,"val":9},"parent":{"$ref":"6"},"right":null,"val":13},"val":7},"val":6},"parent":null,"right":{"$id":"9","left":{"$id":"10","left":null,"parent":{"$ref":"9"},"right":null,"val":17},"parent":{"$ref":"1"},"right":{"$id":"11","left":null,"parent":{"$ref":"9"},"right":null,"val":20},"val":18},"val":15}
p = 15
Output: 17

Example 4:

Input: 
root = {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":{"$id":"4","left":null,"parent":{"$ref":"3"},"right":null,"val":2},"parent":{"$ref":"2"},"right":{"$id":"5","left":null,"parent":{"$ref":"3"},"right":null,"val":4},"val":3},"parent":{"$ref":"1"},"right":{"$id":"6","left":null,"parent":{"$ref":"2"},"right":{"$id":"7","left":{"$id":"8","left":null,"parent":{"$ref":"7"},"right":null,"val":9},"parent":{"$ref":"6"},"right":null,"val":13},"val":7},"val":6},"parent":null,"right":{"$id":"9","left":{"$id":"10","left":null,"parent":{"$ref":"9"},"right":null,"val":17},"parent":{"$ref":"1"},"right":{"$id":"11","left":null,"parent":{"$ref":"9"},"right":null,"val":20},"val":18},"val":15}
p = 13
Output: 15

Note:

If the given node has no in-order successor in the tree, return null.
It’s guaranteed that the values of the tree are unique.
Remember that we are using the Node type instead of TreeNode type so their string representation are different.

Follow up:

Could you solve it without looking up any of the node’s values?

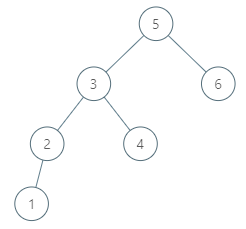
这道题是之前的那道 Inorder Successor in BST 的后续，之前那道题给了我们树的根结点，而这道题并没有确定给我们根结点，只是给了树的任意一个结点，然后让求给定结点的中序后继结点。这道题比较好的一点就是例子给的比较详尽，基本覆盖到了大部分的情况，包括一些很 tricky 的情况。首先来看例子1，结点1的中序后继结点是2，因为中序遍历的顺序是左-根-右。还是例子1，结点2的中序后续结点是3，这样我们就知道中序后续结点可以是其父结点或者右子结点。再看例子2，结点6的中序后续结点是空，因为其已经是中序遍历的最后一个结点了，所以没有后续结点。例子3比较 tricky，结点 15 的中序后续结点不是其右子结点，而是其右子结点的左子结点 17，这样才符合左-根-右的顺序。例子4同样 tricky，结点 13 的中序后继结点并不是其亲生父结点，而是其祖爷爷结点 15。

好，看完了这四个例子，我们应该心里有些数了吧。后继结点出现的位置大致可以分为两类，一类是在子孙结点中，另一类是在祖先结点中。仔细观察例子不难发现，当某个结点存在右子结点时，其中序后继结点就在子孙结点中，反之则在祖先结点中。这样我们就可以分别来处理，当右子结点存在时，我们需要找到右子结点的最左子结点，这个不难，就用个 while 循环就行了。当右子结点不存在，我们就要找到第一个比其值大的祖先结点，也是用个 while 循环去找即可，参见代码如下：

解法一：

class Solution {
public:
    Node* inorderSuccessor(Node* node) {
        if (!node) return nullptr;
        Node *res = nullptr;
        if (node->right) {
            res = node->right;
            while (res && res->left) res = res->left;
        } else {
            res = node->parent;
            while (res && res->val < node->val) res = res->parent;
        }
        return res;
    }
};

本题的 Follow up 让我们不要访问结点值，那么上面的解法就不行了。因为当 node 没有右子结点时，我们没法通过比较结点值来找到第一个大于 node 的祖先结点。虽然不能比较结点值了，我们还是可以通过 node 相对于其 parent 的位置来判断，当 node 是其 parent 的左子结点时，我们知道此时 parent 的结点值一定大于 node，因为这是二叉搜索树的性质。若 node 是其 parent 的右子结点时，则将 node 赋值为其 parent，继续向上找，直到其 parent 结点不存在了，此时说明不存在大于 node 值的祖先结点，这说明 node 是 BST 的最后一个结点了，没有后继结点，直接返回 nullptr 即可，参见代码如下：

解法二：

class Solution {
public:
    Node* inorderSuccessor(Node* node) {
        if (!node) return nullptr;
        if (node->right) {
            node = node->right;
            while (node && node->left) node = node->left;
            return node;
        }
        while (node) {
            if (!node->parent) return nullptr;
            if (node == node->parent->left) return node->parent;
            node = node->parent;
        }
        return node;
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/510

类似题目：

Inorder Successor in BST

参考资料：

https://leetcode.com/problems/inorder-successor-in-bst-ii/

https://leetcode.com/problems/inorder-successor-in-bst-ii/discuss/231587/Java-find-in-parents-or-find-in-descendents

https://leetcode.com/problems/inorder-successor-in-bst-ii/discuss/234295/Java-easy-understanding-well-explained-solution

LeetCode All in One 题目讲解汇总(持续更新中…)

转载请注明来源于 Grandyang 的博客 (grandyang.com)，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 grandyang@qq.com