1352. Product of the Last K Numbers

Design a Skiplist without using any built-in libraries.

A skiplist is a data structure that takes O(log(n)) time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.

For example, we have a Skiplist containing [30,40,50,60,70,90] and we want to add 80 and 45 into it. The Skiplist works this way:

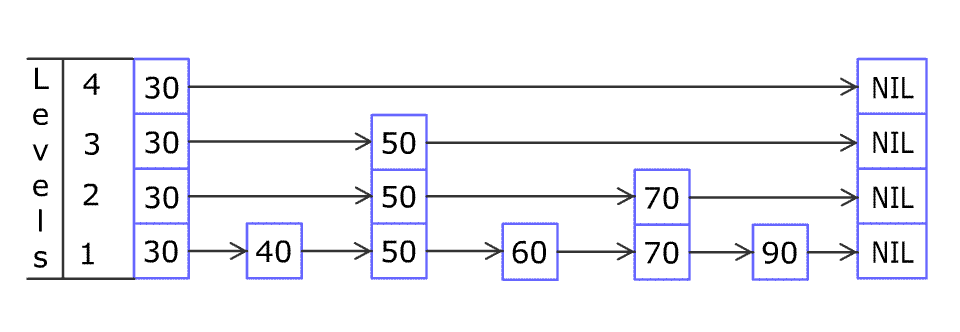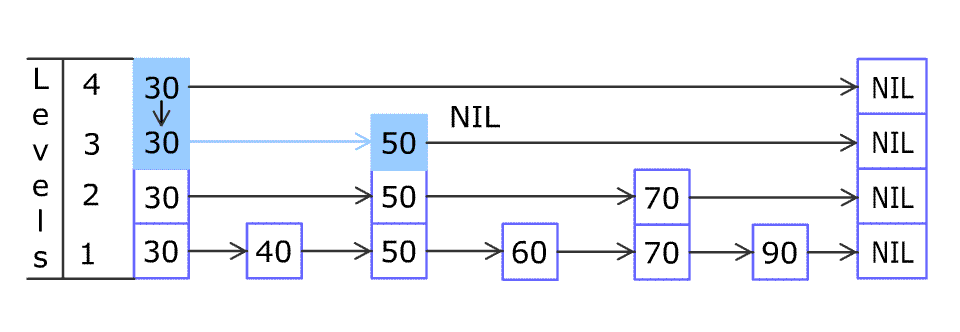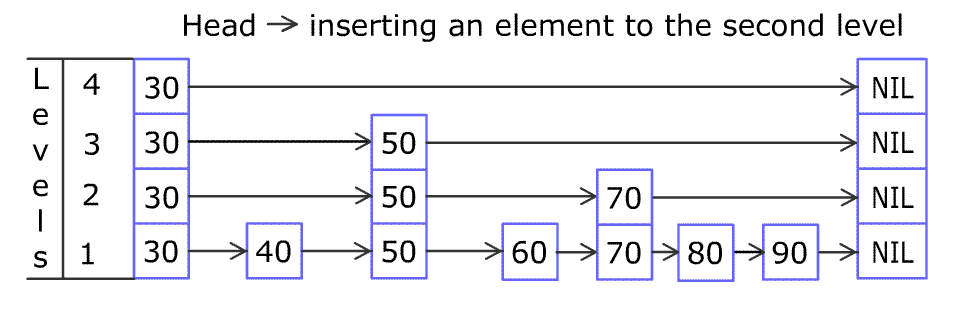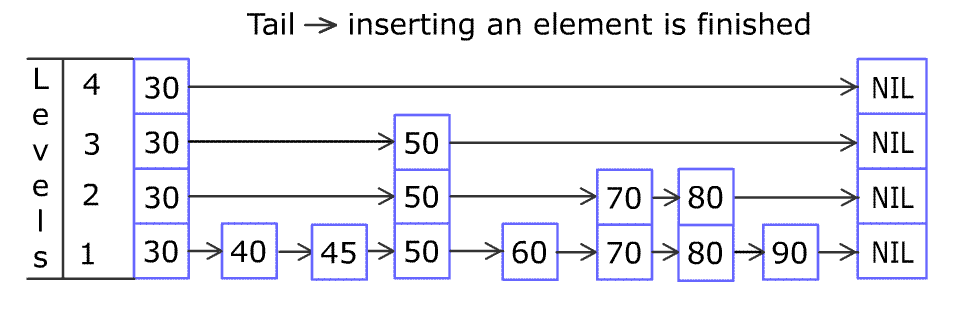
Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than O(n). It can be proven that the average time complexity for each operation is O(log(n)) and space complexity is O(n).

See more about Skiplist: https://en.wikipedia.org/wiki/Skip_list

Implement the Skiplist class:

• Skiplist() Initializes the object of the skiplist.
• bool search(int target) Returns true if the integer target exists in the Skiplist or false otherwise.
• void add(int num) Inserts the value num into the SkipList.
• bool erase(int num) Removes the value num from the Skiplist and returns true. If num does not exist in the Skiplist, do nothing and return false. If there exist multiple num values, removing any one of them is fine.

Note that duplicates may exist in the Skiplist, your code needs to handle this situation.

Example 1:

Input
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
Output
[null, null, null, null, false, null, true, false, true, false]

Explanation
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // return False
skiplist.add(4);
skiplist.search(1); // return True
skiplist.erase(0);  // return False, 0 is not in skiplist.
skiplist.erase(1);  // return True
skiplist.search(1); // return False, 1 has already been erased.

Constraints:

• 0 <= num, target <= 2 * 104
• At most 5 * 104 calls will be made to search, add, and erase.

这道题让实现跳跃链表 Skiplist 的数据结构，所谓的跳跃链表，是一种较为简单的数据结构，与红黑树 Red-Black Tree 一样具有 O(lgn) 的操作时间复杂度，但是实现起来更为简单。根据维基百科 Wikipedia 上的描述，快速的查询效果是通过维护一个多层次的链表实现的，且与前一层（下面一层）链表元素的数量相比，每一层链表中的元素的数量更少。一开始时，算法在最稀疏的层次进行搜索，直至需要查找的元素在该层两个相邻的元素中间。这时，算法将跳转到下一个层次，重复刚才的搜索，直到找到需要查找的元素为止。跳过的元素的方法可以是随机性选择或确定性选择，其中前者更为常见。既然是链表的结构，首先得有结点的数据结构吧，题目中没有帮我们定义，需要自己定义。根据 wikipedia 上的说明，跳跃列表是按层建造的。底层是一个普通的有序链表。每个更高层都充当下面列表的快速通道。可以知道这里的结点需要有两个指针，一个是连向右边结点的 next 指针，还一个就是连向下一层对应结点的 down 指针，当然还需要结点值 val。有了结点的定义，就可以来实现跳跃链表了，在构建函数中初始化头结点 head，有点像一般链表题中都会用到的 dummy 结点，值初始化为 -1，两个指针均为空。

对于 search 函数，新建个结点变量 cur 来遍历链表，若 cur 存在则进行 while 循环，这里希望找到第一个小于目标值 target 的结点，所以要再用一个 while 循环，条件是 cur->next 存在，且其结点值小于 target，则将 cur 更新为 cur->next。循环后判断，若 cur->next 存在，且其值正好等于 target，说明找到了，返回 true。即便是没找到，有可能下层中还会有 target，所以将 cur 更新为 cur->down 继续查找，若所有层都找完了还是没找到，则返回 false。对于 add 函数，这个相对比较麻烦一些，因为可能会在多层增加结点，这里用一个数组所有潜在添加结点的位置，还是要遍历链表，同样是找出第一个小于目标值 num 的结点，然后将此位置加入数组中，继续去下一层查找。当所有潜在位置都找好了之后，就要进行插入操作了，用一个布尔型变量 insert 来标记是否继续插入，循环的条件是 insert 为 true，且数组不为空。取出数组末尾的结点，用给定的 num 新建一个结点，其 next 指针指向取出的末尾结点的下一个结点，down 指针指向新建的结点 down，初始化为空。末尾结点的 next 指向这个新建的结点，此时更新 down 结点也指向这个新建的结点，因为可能要去上一层继续添加。由于底层必须添加，而上层则是随机添加，所以这里相当于要掷个骰子，取个随机数判断其奇偶，若是偶数则继续插入结点。当循环退出了，此时可能是摇到奇数了，或者是潜在的插入位置用完了，此时判断若 insert 仍为 true，则在上方新建一个空层，并将 head 的 next 指向这个空层，down 指向原来的层。对于 erase 函数，新建一个布尔型变量 found 表示是否找到了给定值 num，然后进行跟 search 中类似的操作，不同的是当找到目标值后，不是直接返回 true，而是标记 found 为 true，并且移除目标结点，此时不能直接返回的原因是下层可能还有目标值，还得继续移除，当把所有层都遍历完了之后，就可以返回 found 了，参见代码如下：

class Skiplist {
public:
    Skiplist() {
        head = new Node(-1, nullptr, nullptr);
    }
    
    bool search(int target) {
        Node *cur = head;
        while (cur) {
            while (cur->next && cur->next->val < target) cur = cur->next;
            if (cur->next && cur->next->val == target) return true;
            cur = cur->down;
        }
        return false;
    }
    
    void add(int num) {
        vector<Node*> st;
        Node *cur = head, *down;
        while (cur) {
            while (cur->next && cur->next->val < num) cur = cur->next;
            st.push_back(cur);
            cur = cur->down;
        }
        bool insert = true;
        while (insert && !st.empty()) {
            cur = st.back(); st.pop_back();
            cur->next = new Node(num, cur->next, down);
            down = cur->next;
            insert = (rand() & 1) == 0;
        }
        if (insert) head = new Node(-1, nullptr, head);
    }
    
    bool erase(int num) {
        Node *cur = head;
        bool found = false;
        while (cur) {
            while (cur->next && cur->next->val < num) cur = cur->next;
            if (cur->next && cur->next->val == num) {
                found =  true;
                cur->next = cur->next->next;
            }
            cur = cur->down;
        }
        return found;
    }

private:
    struct Node {
        int val;
        Node *next, *down;
        Node(int val, Node* next, Node* down): val(val), next(next), down(down) {}
    };
    Node *head;
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1206

类似题目：

Design Linked List

Design HashMap

Design HashSet

参考资料：

https://leetcode.com/problems/design-skiplist/

https://leetcode.com/problems/design-skiplist/discuss/947076/Clean-Java

https://leetcode.com/problems/design-skiplist/discuss/400028/C%2B%2B-SkipList.-2-pointer-for-each-node.-64ms.

LeetCode All in One 题目讲解汇总(持续更新中…)

---

转载请注明来源于 Grandyang 的博客 (grandyang.com)，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 grandyang@qq.com