Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.
Example 1:
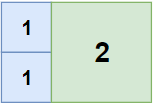
Input: n = 2, m = 3
Output: 3
Explanation: `3` squares are necessary to cover the rectangle.
`2` (squares of `1x1`)
`1` (square of `2x2`)
Example 2:
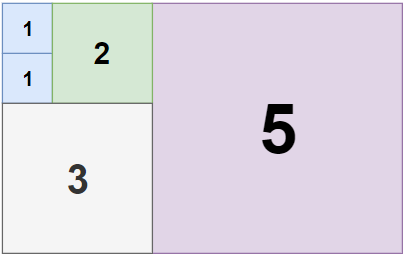
Input: n = 5, m = 8
Output: 5
Example 3:
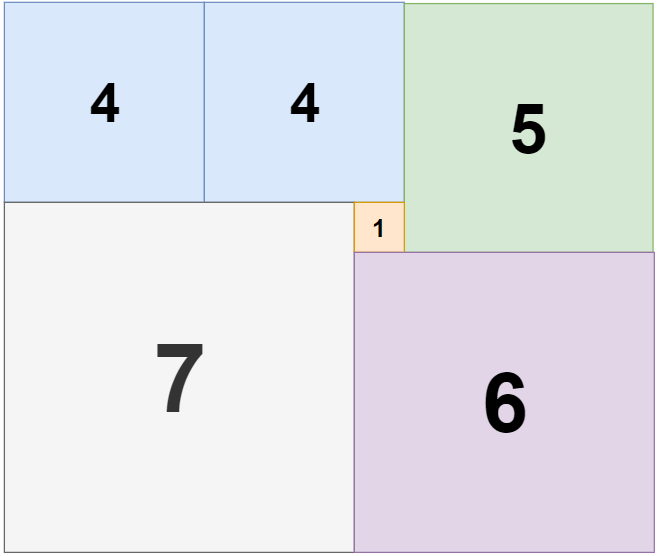
Input: n = 11, m = 13
Output: 6
Constraints:
1 <= n, m <= 13
这道题给了一个 n by m 大小的矩形,问最少可以用多少个正方形填满这个矩形。有点像小时候玩的拼图游戏,用大小不同正方形来拼出一个大的矩形。为了方便分析,这里始终认为n小于等于m,若给定的n大于m,直接调换一下也不影响最终结果。现在来考虑一下如何才能拼出 n by m 大小的矩形,可能大家会下意识的先拿出一个 n by n 的矩形占一大块,然后再拿小矩形去拼 n by (m-n) 的矩形,这种类似贪婪算法的拼法并不能保证全局最优,这种方法在例子1和2中是可以的,但是例子3中就不适用了。由于没有明确的策略去拼,为了得到全局最优解,只有遍历所有情况,取其中的最小值。则第一个正方形可选的范围就是 [1, n],对于其中任意一个值i来说,相当于左下角先放了个 i by i 的正方形,剩下的部分可以分为两个矩形,有两种不同的分法:水平切一刀的话,就分成了 (n-i) by m 的矩形和 i by (m-i) 的矩形;竖直切一刀的话,就分成了 (n-i) by i 的矩形和 n by (m-i) 的矩形,这两种分法都要分别计算一下,参见简陋的下图所示:
m
--------------
|n-i |
n |------------|
| i | m-i |
--------------
m
--------------
|n-i| |
n |---- |
| i | m-i |
--------------
由于分割成的子矩形可以看作是一个子问题的重现,所以这道题用递归来做是非常合适的,同时为了避免大量的重复计算,应该使用记忆数组来保存计算过的值,其中 memo[i][j] 就表示 i by j 的矩形可以用最少的正方形拼出的个数。上面这种分割方法并不能包含所有的情况,比如例子3就无法通过这种方法得到。所以还有一种拼法,是同时在左下角和右上角各放一个正方形,然后再去拼剩余的部分,左下角的正方形边长为i,范围是 [1, n],右上角的正方形边长为j,范围是 [n-i+1, min(m-i, n)]。这里可能会有童鞋有疑问,为啥右上角的正方形边长要从 n-i+1 开始,而不是从1开始呢?这是个好问题,因为这里需要 i+j 大于n,只有这样才能区别于上面两种拼法,否则的话,这种分割方法其实还是包括在前两种分割方法里面的。
当这两个边角正方形大小确定了之后,剩余的部分可能需要分成三个矩形,就像例子3中所示一样,中间还有个迷你矩形,其长宽需要特别计算一下,是个 (i+j-n) by (m-i-j) 的矩形,然后剩下的两个矩形大小分别为 (n-i) by (m-j) 和 (n-j) by (m-i)。这些都理清了之后,代码应该也就不难写了。主要来看递归函数的写法吧,首先判断n和m的大小,若n大于m,则交换两个参数。若n等于0,直接返回0,若n等于m,本身就是个正方形,返回1,若n等于1,则只能用 1 by 1 的正方形来拼,返回m,若 memo[n][m] 值大于0,说明当前情况已经计算过了,直接返回 memo[n][m]。否则开始正式计算,初始化结果 res 为整型最大值,然后遍历左下角先拼的正方的边长,之前说了,范围是 [1, n],然后先计算分成两个矩形的两种情况,分别调用递归,并更新结果 res。然后就是计算右上角再放正方形的情况,其边长范围是 [n-i+1, min(m-i, n)],之前也分析过了,然后对分割出的三个小矩形分别调用递归,并用结果来更新 res 即可,参见代码如下:
class Solution {
public:
int tilingRectangle(int n, int m) {
if (n > m) return tilingRectangle(m, n);
vector<vector<int>> memo(n + 1, vector<int>(m + 1));
return helper(n, m, memo);
}
int helper(int n, int m, vector<vector<int>>& memo) {
if (n > m) return helper(m, n, memo);
if (n == 0) return 0;
if (n == m) return 1;
if (n == 1) return m;
if (memo[n][m] > 0) return memo[n][m];
int res = INT_MAX;
for (int i = 1; i <= n; ++i) {
res = min(res, 1 + helper(n - i, m, memo) + helper(i, m - i, memo));
res = min(res, 1 + helper(n, m - i, memo) + helper(n - i, i, memo));
for (int j = n - i + 1; j < m - i && j < n; ++j) {
res = min(res, 2 + helper(n - i, m - j, memo) + helper(i + j - n, m - i - j, memo) + helper(n - j, m - i, memo));
}
}
return memo[n][m] = res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1240
参考资料:
https://leetcode.com/problems/tiling-a-rectangle-with-the-fewest-squares/
LeetCode All in One 题目讲解汇总(持续更新中…)
喜欢请点赞,疼爱请打赏❤️.
微信打赏
 |
|
Venmo 打赏

—|—
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




