We have two types of tiles: a 2x1 domino shape, and an “L” tromino shape. These shapes may be rotated.
XX <- domino
XX <- "L" tromino
X
Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.
(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)
Example:
Input: 3
Output: 5
Explanation:
The five different ways are listed below, different letters indicates different tiles:
XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY
Note:
- N will be in range
[1, 1000].
这道题是关于多米诺骨牌和三格骨牌的,其中由两个方形格子组成的是多米诺骨牌(音译,即为双格骨牌),而由三个方形格子组成的‘L’型的是三格骨牌,但其实本质还是个拼格子的问题,并没有利用到骨牌酷炫的连倒技能,倒反而更像是俄罗斯方块中的形状。说是有一个2xN大小的棋盘,我们需要用这些多米诺和三格骨牌来将棋盘填满,问有多少种不同的填充方法,结果需要对一个超大数取余。那么根据博主多年的经验,对于这种求极值,并且超大的情况下,只能使用动态规划Dynamic Programming来做,什么暴力递归神马的,等着爆栈吧。
既然决定了要用DP来做,那么首先就来设计dp数组吧,这里我们就用一个一维的dp数组就行了,其中dp[i]表示填满前i列的不同填法总数对超大数10e^9+7取余后的结果。那么DP解法的难点就是求状态转移方程了,没什么太好的思路的时候,就从最简单的情况开始罗列吧。题目中给了N的范围是[1, 1000],那么我们来看:
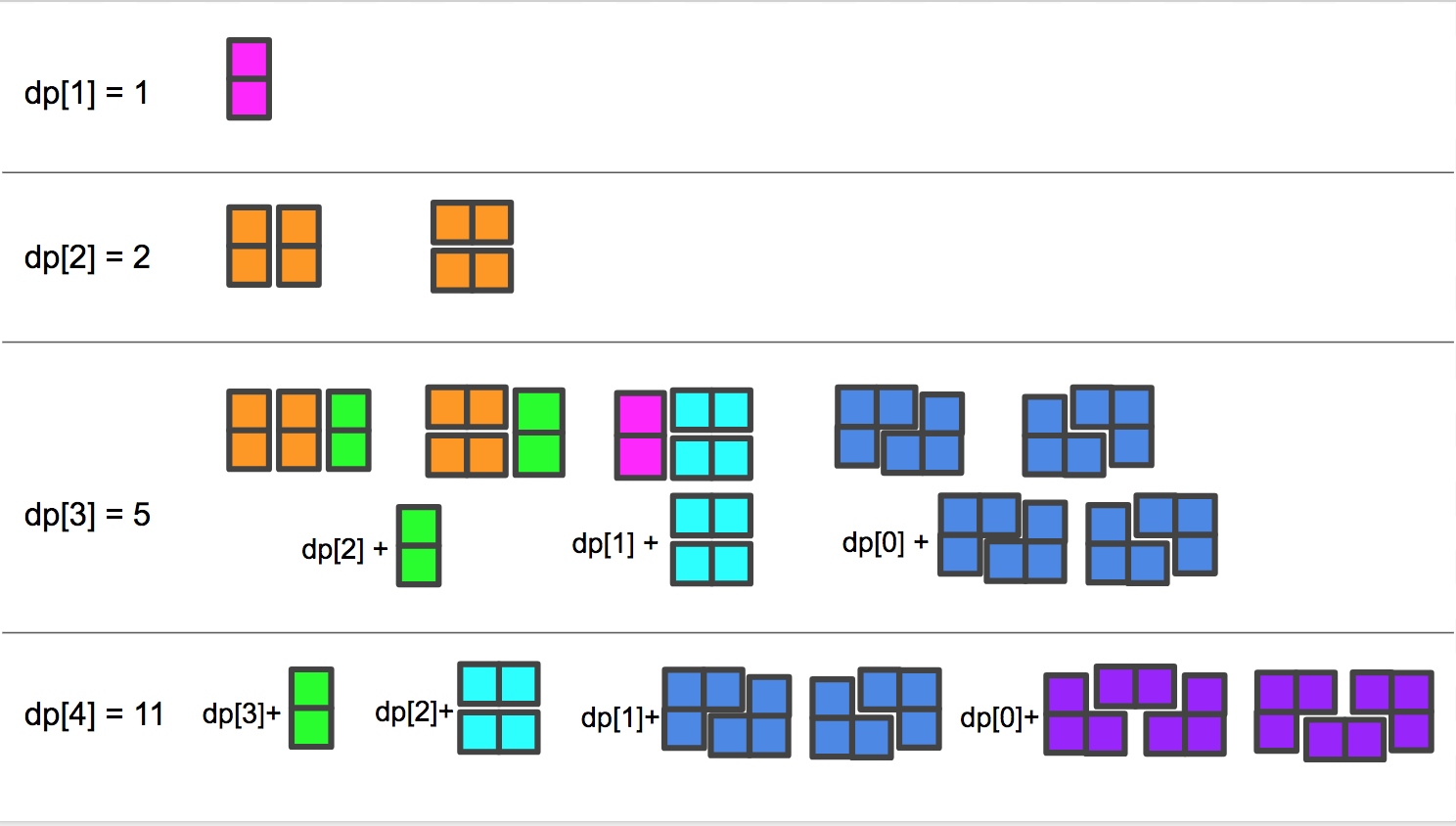
当N=1时,那么就是一个2x1大小的棋盘,只能放一个多米诺骨牌,只有一种情况。
当N=2时,那么就是一个2x2大小的棋盘,如下图所示,我们有两种放置方法,可以将两个多米诺骨牌竖着并排放,或者是将其横着并排放。
当N=3时,那么就是一个3x2大小的棋盘,我们共用五种放置方法,如下图所示。仔细观察这五种情况,我们发现其时时跟上面的情况有联系的。前两种情况其实是N=2的两种情况后面加上了一个竖着的多米诺骨牌,第三种情况其实是N=1的那种情况后面加上了两个平行的横向的多米诺骨牌,后两种情况是N=0(空集)再加上两种三格骨牌对角摆开的情况。
当N=4时,那么就是一个4x2大小的棋盘,我们共用十一种放置方法,太多了就不一一画出来了,但是其也是由之前的情况组合而成的。首先是N=3的所有情况后面加上一个竖着多米诺骨牌,然后是N=2的所有情况加上两个平行的横向的多米诺骨牌,然后N=1再加上两种三格骨牌对角摆开的情况,然后N=0(空集)再加上两种三格骨牌和一个横向多米诺骨牌组成的情况。
N=5的情况博主没有再画了,可以参见ZhengKaiWei大神的帖子中的手稿图,很萌~
根据目前的状况,我们可以总结一个很重要的规律,就是dp[n]是由之前的dp值组成的,其中 dp[n-1] 和 dp[n-2] 各自能贡献一种组成方式,而dp[n-3],一直到dp[0],都能各自贡献两种组成方式,所以状态转移方程呼之欲出:
dp[n] = dp[n-1] + dp[n-2] + 2 * (dp[n-3] + … + dp[0])
= dp[n-1] + dp[n-3] + dp[n-2] + dp[n-3] + 2 * (dp[n-4] + … dp[0])
= dp[n-1] + dp[n-3] + dp[n-1]
= 2 * dp[n-1] + dp[n-3]
最后化简后的形式就是最终的状态转移方程了,是不是叼的飞起~
class Solution {
public:
int numTilings(int N) {
int M = 1e9 + 7;
vector<long> dp(N + 1);
dp[0] = 1; dp[1] = 1; dp[2] = 2;
for (int i = 3; i <= N; ++i) {
dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % M;
}
return dp[N];
}
};
参考资料:
https://leetcode.com/problems/domino-and-tromino-tiling/discuss/116513/Java-solution-DP
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




