You are given a doubly linked list which in addition to the next and previous pointers, it could have a child pointer, which may or may not point to a separate doubly linked list. These child lists may have one or more children of their own, and so on, to produce a multilevel data structure, as shown in the example below.
Flatten the list so that all the nodes appear in a single-level, doubly linked list. You are given the head of the first level of the list.
Example:
Input:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
Output:
1-2-3-7-8-11-12-9-10-4-5-6-NULL
Explanation for the above example:
Given the following multilevel doubly linked list:
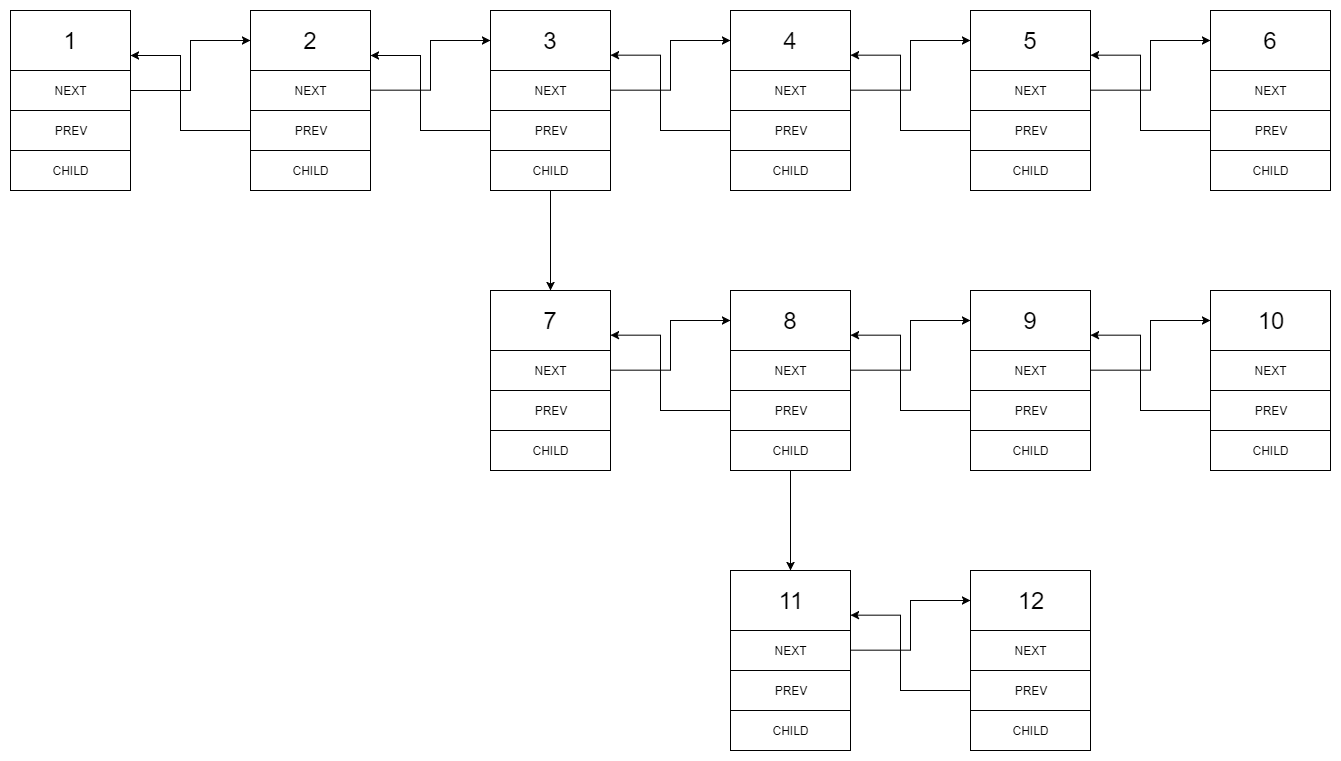
We should return the following flattened doubly linked list:

这道题给了一个多层的双向链表,让我们压平成为一层的双向链表,题目中给了形象的图例,不难理解题意。根据题目中给的例子,我们可以看出如果某个结点有下一层双向链表,那么下一层双向链表中的结点就要先加入进去,如果下一层链表中某个结点还有下一层,那么还是优先加入下一层的结点,整个加入的机制是DFS的,就是有岔路先走岔路,走到没路了后再返回,这就是深度优先遍历的机制。好,那么既然是DFS,肯定优先考虑递归啦。方法有了,再来看具体怎么递归。由于给定的多层链表本身就是双向的,所以我们只需要把下一层的结点移到第一层即可,那么没有子结点的结点就保持原状,不作处理。只有对于那些有子结点的,我们需要做一些处理,由于子结点链接的双向链表要加到后面,所以当前结点之后要断开,再断开之前,我们用变量 next 指向下一个链表,然后对子结点调用递归函数,我们 suppose 返回的结点已经压平了,那么就只有一层,就相当于要把这一层的结点加到断开的地方,所以需要知道这层的最后一个结点的位置,我们用一个变量 last,来遍历到压平的这一层的末结点。现在就可以开始链接了,首先把子结点链到 cur 的 next,然后把反向指针 prev 也链上。此时 cur 的子结点 child 可以清空,然后压平的这一层的末节点 last 链上之前保存的 next 结点,如果 next 非空,那么链上反向结点 prev。这些操作完成后,我们就已经将压平的这一层完整的加入了之前层断开的地方,继续在之前层往下遍历即可,参见代码如下:
解法一:
class Solution {
public:
Node* flatten(Node* head) {
Node *cur = head;
while (cur) {
if (cur->child) {
Node *next = cur->next;
cur->child = flatten(cur->child);
Node *last = cur->child;
while (last->next) last = last->next;
cur->next = cur->child;
cur->next->prev = cur;
cur->child = NULL;
last->next = next;
if (next) next->prev = last;
}
cur = cur->next;
}
return head;
}
};
我们其实也可以不用递归,链表的题不像树的题,对于树的题使用递归可以很简洁,而链表递归和迭代可能差的并不多。如果你仔细对比两种方法的代码,你会发现迭代的写法刚好比递归的写法少了调用递归的那一行,给人一种完全没有必要使用递归的感觉,其实两种解法的操作顺序不同的,递归写法是从最底层开始操作,先把最底层加入倒数第二层,再把混合后的层加入倒数第三层,依此类推,直到都融合到第一层为止。而迭代的写法却是反过来的,先把第二层加入第一层,此时第二层底下可能还有很多层,不必理会,之后等遍历到的时候,再一层一层的加入第一层中,不管哪种方法,最终都可以压平,参见代码如下:
解法二:
class Solution {
public:
Node* flatten(Node* head) {
Node *cur = head;
while (cur) {
if (cur->child) {
Node *next = cur->next;
Node *last = cur->child;
while (last->next) last = last->next;
cur->next = cur->child;
cur->next->prev = cur;
cur->child = NULL;
last->next = next;
if (next) next->prev = last;
}
cur = cur->next;
}
return head;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/430
类似题目:
Flatten Binary Tree to Linked List
参考资料:
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




