In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the ith domino, so that A[i] and B[i] swap values.
Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.
If it cannot be done, return -1.
Example 1:
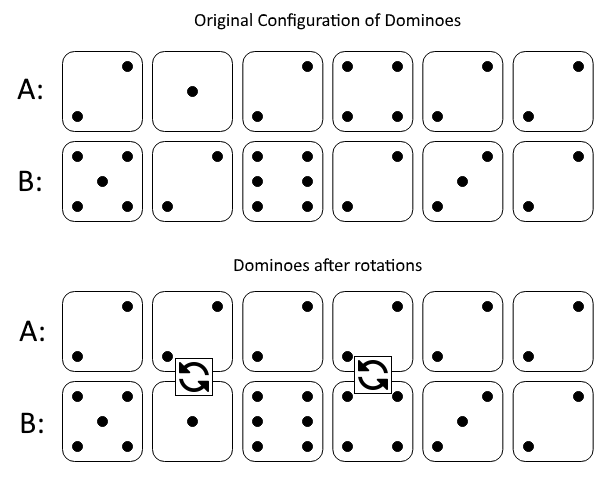
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
Example 2:
Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints:
2 <= A.length == B.length <= 2 * 1041 <= A[i], B[i] <= 6
这道题说是有长度相等的两个数组A和B,分别表示一排多米诺的上边数字和下边数字,多米诺的个数和数组的长度相同,数字为1到6之间,问最少旋转多少次多米诺,可以使得上边或下边的数字全部相同。例子1中给了图解,很好的帮我们理解题意,实际上出现次数越多的数字越可能就是最终全部相同的数字,所以统计A和B中每个数字出现的次数就变的很重要了,由于A和B中有可能相同位置上的是相同的数字,则不用翻转,要使得同一行变为相同的数字,翻转的地方必须是不同的数字,如何才能知道翻转后可以使同一行完全相同呢?需要某个数字在A中出现的次数加上在B中出现的次数减去A和B中相同位置出现的次数后正好等于数组的长度,这里就需要用三个数组 cntA,cntB,和 same 来分别记录某个数字在A中,B中,A和B相同位置上出现的个数,然后遍历1到6,只要符合上面提到的条件,就可以直接返回数组长度减去该数字在A和B中出现的次数中的较大值,参见代码如下:
class Solution {
public:
int minDominoRotations(vector<int>& A, vector<int>& B) {
int res = INT_MAX, n = A.size();
vector<int> cntA(7), cntB(7), same(7);
for (int i = 0; i < n; ++i) {
++cntA[A[i]];
++cntB[B[i]];
if (A[i] == B[i]) ++same[A[i]];
}
for (int i = 1; i <= 6; ++i) {
if (cntA[i] + cntB[i] - same[i] == n) {
return n - max(cntA[i], cntB[i]);
}
}
return -1;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1007
参考资料:
https://leetcode.com/problems/minimum-domino-rotations-for-equal-row/
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




