1260. Shift 2D Grid

置顶

Created At : 2023-10-28 15:14

Count:722 Views 👀 :

Comment:

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

Element at grid[i][j] moves to grid[i][j + 1].
Element at grid[i][n - 1] moves to grid[i + 1][0].
Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

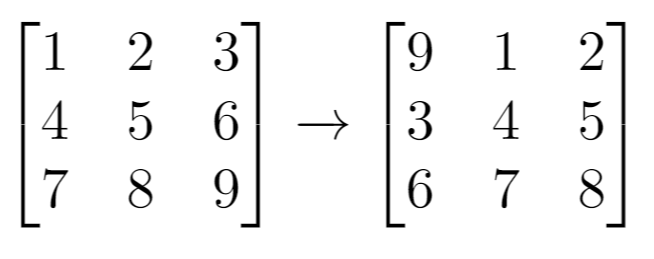
Input: `grid` = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

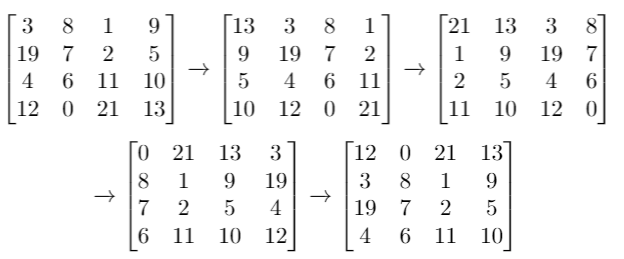
Input: `grid` = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: `grid` = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

m == grid.length
n == grid[i].length
1 <= m <= 50
1 <= n <= 50
-1000 <= grid[i][j] <= 1000
0 <= k <= 100

这道题让移动一个二维数组，移动方法是水平移动，即每个元素向右平移一位，行末尾的元素移动到下一行的开头，数组最后一个元素移动到开头的第一个元素，像这样移动k次，返回最终的数组。由于要移动k次，若每次都更新一遍数组的值，实在是不高效，最好直接能计算出最终状态的值，那么关注点就是计算一个元素水平移动k次的新位置。由于是二维数组，所以总是存在一个换行的问题，比较麻烦，一个很好的 trick 就是先将数组拉平，变成一维数组，这样移动k位就很方便，唯一需要注意是加k后可能超过一维数组的范围，需要当作循环数组来处理。明白了思路，代码就很好写了，新建一个和原数组同等大小的数组 res，然后遍历原数组，对于每个位置 (i, j)，计算其在拉平后的一维数组中的位置 i*n + j，然后再加上平移k，为了防止越界，最后再对 m*n 取余，得到了其在一维数组中的位置，将其转回二维数组的坐标，并更新结果 res 中的对应位置即可，参见代码如下：

class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int m = grid.size(), n = grid[0].size(), len = m * n;
        vector<vector<int>> res(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int idx = (i * n + j + k) % len;
                res[idx / n][idx % n] = grid[i][j];
            }
        }
        return res;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1260

参考资料：

https://leetcode.com/problems/shift-2d-grid/

https://leetcode.com/problems/shift-2d-grid/discuss/458848/C%2B%2B-Straight-forward-solution

https://leetcode.com/problems/shift-2d-grid/discuss/431102/JavaPython-3-2-simple-codes-using-mod-space-O(1).

LeetCode All in One 题目讲解汇总(持续更新中…)

喜欢请点赞，疼爱请打赏❤️.

微信打赏