We are given a binary tree (with root node root), a target node, and an integer value K.
Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.
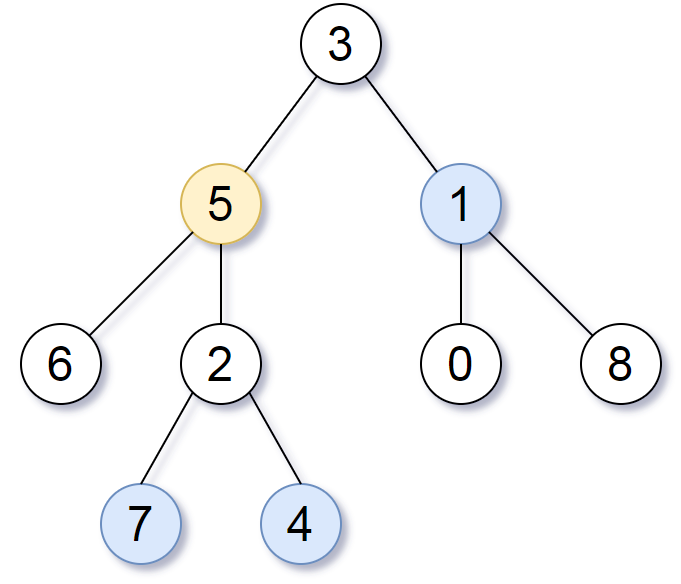
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
Output: [7,4,1]
Explanation:
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.
Note that the inputs “root” and “target” are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.
Note:
- The given tree is non-empty.
- Each node in the tree has unique values
0 <= node.val <= 500. - The
targetnode is a node in the tree. 0 <= K <= 1000.
这道题给了我们一棵二叉树,一个目标结点 target,还有一个整数K,让返回所有跟目标结点 target 相距K的结点。我们知道在子树中寻找距离为K的结点很容易,因为只需要一层一层的向下遍历即可,难点就在于符合题意的结点有可能是祖先结点,或者是在旁边的兄弟子树中,这就比较麻烦了,因为二叉树只有从父结点到子结点的路径,反过来就不行。既然没有,我们就手动创建这样的反向连接即可,这样树的遍历问题就转为了图的遍历(其实树也是一种特殊的图)。建立反向连接就是用一个 HashMap 来来建立每个结点和其父结点之间的映射,使用先序遍历建立好所有的反向连接,然后再开始查找和目标结点距离K的所有结点,这里需要一个 HashSet 来记录所有已经访问过了的结点。
在递归函数中,首先判断当前结点是否已经访问过,是的话直接返回,否则就加入到 visited 中。再判断此时K是否为0,是的话说明当前结点已经是距离目标结点为K的点了,将其加入结果 res 中,然后直接返回。否则分别对当前结点的左右子结点调用递归函数,注意此时带入 K-1,这两步是对子树进行查找。之前说了,还得对父结点,以及兄弟子树进行查找,这是就体现出建立的反向连接 HashMap 的作用了,若当前结点的父结点存在,我们也要对其父结点调用递归函数,并同样带入 K-1,这样就能正确的找到所有满足题意的点了,参见代码如下:
解法一:
class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
if (!root) return {};
vector<int> res;
unordered_map<TreeNode*, TreeNode*> parent;
unordered_set<TreeNode*> visited;
findParent(root, parent);
helper(target, K, parent, visited, res);
return res;
}
void findParent(TreeNode* node, unordered_map<TreeNode*, TreeNode*>& parent) {
if (!node) return;
if (node->left) parent[node->left] = node;
if (node->right) parent[node->right] = node;
findParent(node->left, parent);
findParent(node->right, parent);
}
void helper(TreeNode* node, int K, unordered_map<TreeNode*, TreeNode*>& parent, unordered_set<TreeNode*>& visited, vector<int>& res) {
if (visited.count(node)) return;
visited.insert(node);
if (K == 0) {res.push_back(node->val); return;}
if (node->left) helper(node->left, K - 1, parent, visited, res);
if (node->right) helper(node->right, K - 1, parent, visited, res);
if (parent[node]) helper(parent[node], K - 1, parent, visited, res);
}
};
既然是图的遍历,那就也可以使用 BFS 来做,为了方便起见,我们直接建立一个邻接链表,即每个结点最多有三个跟其相连的结点,左右子结点和父结点,使用一个 HashMap 来建立每个结点和其相邻的结点数组之间的映射,这样就几乎完全将其当作图来对待了,建立好邻接链表之后,原来的树的结构都不需要用了。既然是 BFS 进行层序遍历,就要使用队列 queue,还要一个 HashSet 来记录访问过的结点。在 while 循环中,若K为0了,说明当前这层的结点都是符合题意的,就把当前队列中所有的结点加入结果 res,并返回即可。否则就进行层序遍历,取出当前层的每个结点,并在邻接链表中找到和其相邻的结点,若没有访问过,就加入 visited 和 queue 中即可。记得每层遍历完成之后,K要自减1,参见代码如下:
解法二:
class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
if (!root) return {};
vector<int> res;
unordered_map<TreeNode*, vector<TreeNode*>> m;
queue<TreeNode*> q{{target}};
unordered_set<TreeNode*> visited{{target}};
findParent(root, NULL, m);
while (!q.empty()) {
if (K == 0) {
for (int i = q.size(); i > 0; --i) {
res.push_back(q.front()->val); q.pop();
}
return res;
}
for (int i = q.size(); i > 0; --i) {
TreeNode *t = q.front(); q.pop();
for (TreeNode *node : m[t]) {
if (visited.count(node)) continue;
visited.insert(node);
q.push(node);
}
}
--K;
}
return res;
}
void findParent(TreeNode* node, TreeNode* pre, unordered_map<TreeNode*, vector<TreeNode*>>& m) {
if (!node) return;
if (m.count(node)) return;
if (pre) {
m[node].push_back(pre);
m[pre].push_back(node);
}
findParent(node->left, node, m);
findParent(node->right, node, m);
}
};
其实这道题也可以不用 HashMap,不建立邻接链表,直接在递归中完成所有的需求,真正体现了递归的博大精深。在进行递归之前,我们要先判断一个 corner case,那就是当 K==0 时,此时要返回的就是目标结点值本身,可以直接返回。否则就要进行递归了。这里的递归函数跟之前的有所不同,是需要返回值的,这个返回值表示的含义比较复杂,若为0,表示当前结点为空或者当前结点就是距离目标结点为K的点,此时返回值为0,是为了进行剪枝,使得不用对其左右子结点再次进行递归。当目标结点正好是当前结点的时候,递归函数返回值为1,其他的返回值为当前结点离目标结点的距离加1。还需要一个参数 dist,其含义为离目标结点的距离,注意和递归的返回值区别,这里不用加1,且其为0时候不是为了剪枝,而是真不知道离目标结点的距离。
在递归函数中,首先判断若当前结点为空,则直接返回0。然后判断 dist 是否为k,是的话,说目标结点距离当前结点的距离为K,是符合题意的,需要加入结果 res 中,并返回0,注意这里返回0是为了剪枝。否则判断,若当前结点正好就是目标结点,或者已经遍历过了目标结点(表现为 dist 大于0),那么对左右子树分别调用递归函数,并将返回值分别存入 left 和 right 两个变量中。注意此时应带入 dist+1,因为是先序遍历,若目标结点之前被遍历到了,那么说明目标结点肯定不在当前结点的子树中,当前要往子树遍历的话,肯定离目标结点又远了一些,需要加1。若当前结点不是目标结点,也还没见到目标结点时,同样也需要对左右子结点调用递归函数,但此时 dist 不加1,因为不确定目标结点的位置。若 left 或者 right 值等于K,则说明目标结点在子树中,且距离当前结点为K(为啥呢?因为目标结点本身是返回1,所以当左右子结点返回K时,和当前结点距离是K)。接下来判断,若当前结点是目标结点,直接返回1,这个前面解释过了。然后再看 left 和 right 的值是否大于0,若 left 值大于0,说明目标结点在左子树中,我们此时就要对右子结点再调用一次递归,并且 dist 带入 left+1,同理,若 right 值大于0,说明目标结点在右子树中,我们此时就要对左子结点再调用一次递归,并且 dist 带入 right+1。这两步很重要,是之所以能不建立邻接链表的关键所在。若 left 大于0,则返回 left+1,若 right 大于0,则返回 right+1,否则就返回0,参见代码如下:
解法三:
class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
if (K == 0) return {target->val};
vector<int> res;
helper(root, target, K, 0, res);
return res;
}
int helper(TreeNode* node, TreeNode* target, int k, int dist, vector<int>& res) {
if (!node) return 0;
if (dist == k) {res.push_back(node->val); return 0;}
int left = 0, right = 0;
if (node->val == target->val || dist > 0) {
left = helper(node->left, target, k, dist + 1, res);
right = helper(node->right, target, k, dist + 1, res);
} else {
left = helper(node->left, target, k, dist, res);
right = helper(node->right, target, k, dist, res);
}
if (left == k || right == k) {res.push_back(node->val); return 0;}
if (node->val == target->val) return 1;
if (left > 0) helper(node->right, target, k, left + 1, res);
if (right > 0) helper(node->left, target, k, right + 1, res);
if (left > 0 || right > 0) return left > 0 ? left + 1 : right + 1;
return 0;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/863
参考资料:
https://leetcode.com/problems/all-nodes-distance-k-in-binary-tree/
https://leetcode.com/problems/all-nodes-distance-k-in-binary-tree/discuss/143752/JAVA-Graph-%2B-BFS
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




