74. Search a 2D Matrix

置顶

Created At : 2021-06-18 07:56

Count:1.1k Views 👀 :

Comment:

You are given an m x n integer matrix matrix with the following two properties:

Each row is sorted in non-decreasing order.
The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

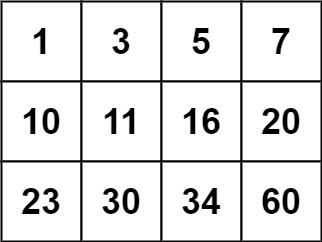
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10^4 <= matrix[i][j], target <= 10^4

这道题要求搜索一个二维矩阵，由于给的矩阵是有序的，所以很自然的想到要用二分查找法，可以在第一列上先用一次二分查找法找到目标值所在的行的位置，然后在该行上再用一次二分查找法来找是否存在目标值。对于第一个二分查找，由于第一列的数中可能没有 target 值，该如何查找呢，是博主之前的总结帖 LeetCode Binary Search Summary 二分搜索法小结中的哪一类呢？

如果是查找第一个不小于目标值的数，当 target 在第一列时，会返回 target 所在的行，但若 target 不在的话，有可能会返回下一行，不好统一。所以可以查找第一个大于目标值的数，也就是总结帖中的第三类，这样只要回退一个，就一定是 target 所在的行。但需要注意的一点是，如果返回的是0，就不能回退了，以免越界，记得要判断一下。找到了 target 所在的行数，就可以再次使用二分搜索，此时就是总结帖中的第一类了，查找和 target 值相同的数，也是最简单的一类，分分钟搞定即可，参见代码如下：

解法一：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int left = 0, right = matrix.size();
        while (left < right) {
            int mid = (left + right) / 2;
            if (matrix[mid][0] == target) return true;
            if (matrix[mid][0] < target) left = mid + 1;
            else right = mid;
        }
        int tmp = (right > 0) ? (right - 1) : right;
        left = 0;
        right = matrix[tmp].size();
        while (left < right) {
            int mid = (left + right) / 2;
            if (matrix[tmp][mid] == target) return true;
            if (matrix[tmp][mid] < target) left = mid + 1;
            else right = mid;
        }
        return false;
    }
};

当然这道题也可以使用一次二分查找法，如果我们按S型遍历该二维数组，可以得到一个有序的一维数组，只需要用一次二分查找法，而关键就在于坐标的转换，如何把二维坐标和一维坐标转换是关键点，把一个长度为n的一维数组转化为 mn 的二维数组 (mn = n)后，那么原一维数组中下标为i的元素将出现在二维数组中的 [i/n][i%n] 的位置，有了这一点，代码很好写出来了：

解法二：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int left = 0, right = m * n;
        while (left < right) {
            int mid = (left + right) / 2;
            if (matrix[mid / n][mid % n] == target) return true;
            if (matrix[mid / n][mid % n] < target) left = mid + 1;
            else right = mid;
        }
        return false;
    }
};

这道题其实也可以不用二分搜索法，直接使用双指针也是可以的，i指向0，j指向列数，这样第一个被验证的数就是二维数组右上角的数字，假如这个数字等于 target，直接返回 true；若大于 target，说明要减小数字，则列数j自减1；若小于 target，说明要增加数字，行数i自增1。若 while 循环退出了还是没找到 target，直接返回 false 即可，参见代码如下：

解法三：

// Time Complexity O(m + n)
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int i = 0, j = (int)matrix[0].size() - 1;
        while (i < matrix.size() && j >= 0) {
            if (matrix[i][j] == target) return true;
            if (matrix[i][j] > target) --j;
            else ++i;
        }   
        return false;
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/74

类似题目：

Search a 2D Matrix II

Split Message Based on Limit

参考资料：

https://leetcode.com/problems/search-a-2d-matrix/

https://leetcode.com/problems/search-a-2d-matrix/discuss/26292/Java-clear-solution

https://leetcode.com/problems/search-a-2d-matrix/discuss/26220/Don't-treat-it-as-a-2D-matrix-just-treat-it-as-a-sorted-list

LeetCode All in One 题目讲解汇总(持续更新中…)

（欢迎加入博主的知识星球，博主将及时答疑解惑，并分享刷题经验与总结，快快加入吧～）

喜欢请点赞，疼爱请打赏❤️.