1340. Jump Game V

置顶

Created At : 2023-10-28 15:14

Count:1.2k Views 👀 :

Given an array of integers arr and an integer d. In one step you can jump from index i to index:

i + x where: i + x < arr.length and 0 < x <= d.
i - x where: i - x >= 0 and 0 < x <= d.

In addition, you can only jump from index i to index j if arr[i] > arr[j] and arr[i] > arr[k] for all indices k between i and j (More formally min(i, j) < k < max(i, j)).

You can choose any index of the array and start jumping. Return the maximum number of indices you can visit.

Notice that you can not jump outside of the array at any time.

Example 1:

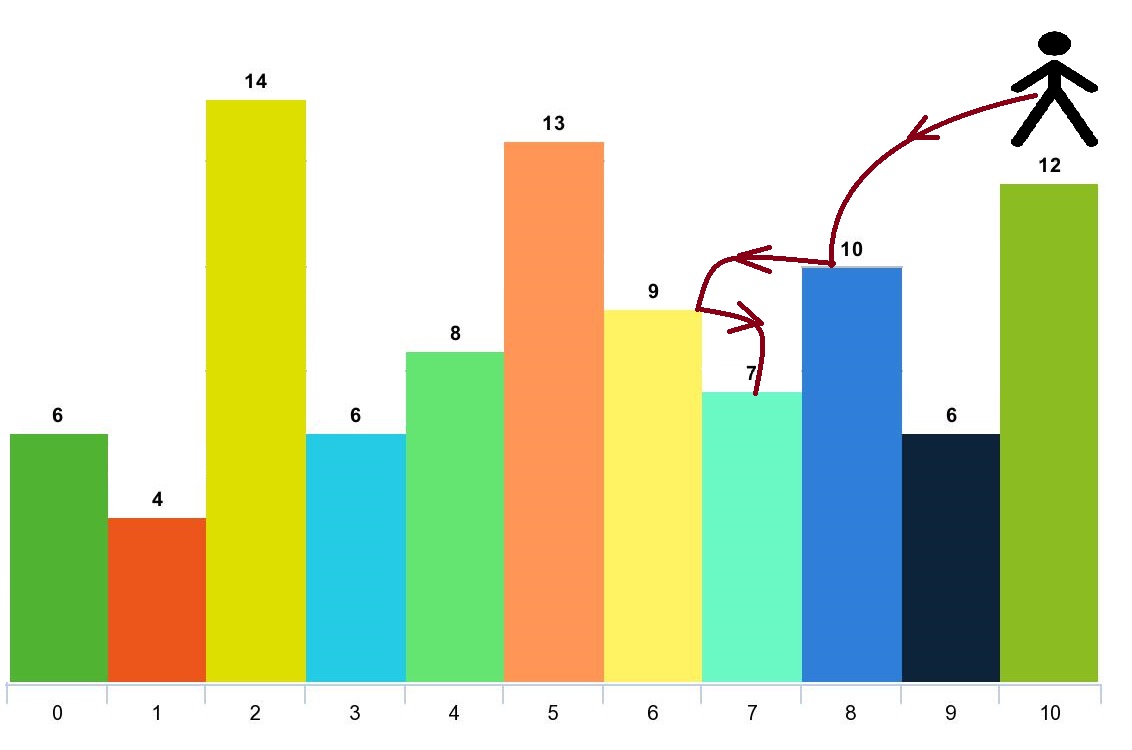
Input: arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
Output: 4
Explanation: You can start at index 10. You can jump 10 –> 8 –> 6 –> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.

Example 2:

Input: arr = [3,3,3,3,3], d = 3
Output: 1
Explanation: You can start at any index. You always cannot jump to any index.

Example 3:

Input: arr = [7,6,5,4,3,2,1], d = 1
Output: 7
Explanation: Start at index 0. You can visit all the indicies.

Constraints:

1 <= arr.length <= 1000
1 <= arr[i] <= 105
1 <= d <= arr.length

这道题是 Jump Game 系列的第五道题，跳跃的方式是这样的，给了一个数组 arr，里面的数字代表高度，还有一个整型数d，表示一次跳跃的最远距离，在任意一个位置可以往左右两个方向跳跃，但是跳跃经过的位置必须都低于起跳位置，且距离不能超过d，现在说是可以从任意位置起跳，让返回最多可以到达的不同位置的数量。既然要找最多的不同位置的数量，而且起跳点又不固定，则肯定是要计算所有情况的，即每个点都要充当起跳点。又因为没有整体跳跃总数的限制，则跳到一个新的位置之后，从该位置开始起跳能到达的位置个数，跟以该位置为起跳点能到达的位置个数相同，这是因为每次都是从高点往低点跳，新的跳跃位置不会跟之前的重复。那么为了避免重复计算，最好可以用一个数组来记录以任意点为起跳点可以到达的位置总数，这里使用一个一维数组 memo，其中 memo[i] 表示以位置i为起跳点，可以到达的位置总数。

由于需要以每个位置都当作起跳点，则可以遍历整个数组，对于每个位置都计算一下可以到达位置的总数，为了方便起见，用一个递归函数来计算，在每个位置计算后返回的值中取最大的，就是题目所求了。现在来看递归函数的实现，由于前面定义了 memo 数组，则对于给定的起跳位置i，首先去 memo 数组中查看，若有值，则说明之前计算过，直接返回其值即可。否则需要另行计算，计算方法也不难，先往右边遍历，不能超过距离限制d，也不能越右边界，对于新跳到的位置，再次调用递归函数，则可以用1加上递归函数的返回值来更新结果 res。同理，再往左遍历，不能超过距离限制d，不能越左边界，对于新跳到的位置，再次调用递归函数，则可以用1加上递归函数的返回值来更新结果 res。这样，最终得到的结果 res 就是以位置i为起跳点，最多可以到达的位置总数了，将其赋值给 memo[i]，并返回即可，参见代码如下：

class Solution {
public:
    int maxJumps(vector<int>& arr, int d) {
        int res = 1, n = arr.size();
        vector<int> memo(1001);
        for (int i = 0; i < n; ++i) {
            res = max(res, dfs(arr, d, i, memo));
        }
        return res;
    }
    int dfs(vector<int>& arr, int d, int i, vector<int>& memo) {
        if (memo[i]) return memo[i];
        int res = 1, n = arr.size();
        for (int j = i + 1; j <= min(i + d, n - 1) && arr[j] < arr[i]; ++j) {
            res = max(res, 1 + dfs(arr, d, j, memo));
        }
        for (int j = i - 1; j >= max(0, i - d) && arr[j] < arr[i]; --j) {
            res = max(res, 1 + dfs(arr, d, j, memo));
        }
        return memo[i] = res;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1340

类似题目：

Jump Game

Jump Game II

Jump Game III

Jump Game IV

Jump Game VI

Jump Game VII

Jump Game VIII

参考资料：

https://leetcode.com/problems/jump-game-v/