Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.
Note that you need to maximize the answer before taking the mod and not after taking it.
Example 1:
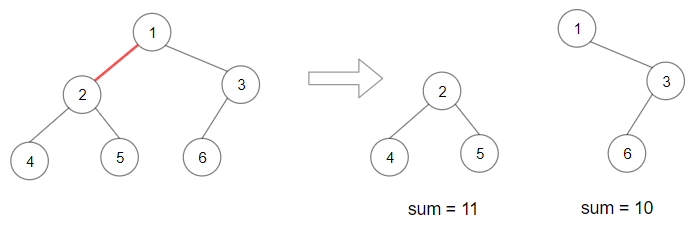
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Example 2:
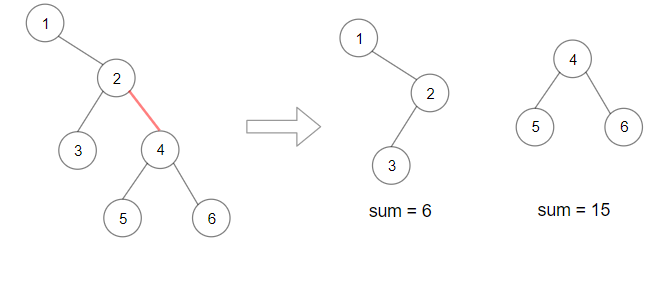
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Constraints:
- The number of nodes in the tree is in the range
[2, 5 * 104]. 1 <= Node.val <= 104
这道题给了一棵二叉树,说是可以移除任意一条边,将其分成两棵子树,需要将二棵子树的结点值分别都加起来,然后相乘,让返回可能最大的乘数,并对一个超大数取余。首先来分析,既然要找到那个最大值,则一定要遍历每一种情况,即计算断开每一条边的情况。那么难点就变成了如何能快速得到断开形成的两棵子树的结点值之和。通过分析例子1可以看出,断开后的左边部分形成了根结点为2的一棵新的二叉树,需要知道其所有结点之和。
此时不难想到,若可以知道以任意结点为根结点的子树的结点之和,会大大利于计算。而后序遍历正好符合这种从底向上遍历的顺序,从叶结点开始,不停的往根结点遍历,同时可以累加遍历到的结点值,这样到达根结点时,就可以得到所有的结点值之和了。博主最开始想到的方法是建立每个结点跟以其为根结点的子树的结点和之间的映射,由于只看了例子1,认为计算乘积的方法就是结点1的映射值减去结点2的映射值,再乘以结点2的映射值就行了。但其实这种方法是不对的,只有在拆分与根结点相连的边的时候才行,比如例子2,拆分位置结点2的映射值是不包括结点1的,所以计算的结果肯定不对。
正确的方法是用整个树所有的结点值之和,减去断开点为根结点的子树之和,所以先要求出所有的结点之和,这里可以快速用一个先序遍历来得到,然后再用一个后序遍历来计算乘积,该递归函数的返回值是以输入的结点为根结点的子树的结点之和,乘积保存在引用参数 res 里。在后序遍历中,首先判空,若当前结点为空,则返回0,否则计算以当前结点为根结点的子树的结点之和,方法是当前结点值加上对左子结点调用递归的返回值,再加上对右子结点调用参数的返回值。此时更新乘积结果 res,用上面算出的结果 cur,乘以整个树结点之和 sum 减去 cur 的值即可,参见代码如下:
解法一:
class Solution {
public:
int maxProduct(TreeNode* root) {
long res = 0, sum = 0, M = 1e9 + 7;
dfs(root, sum);
helper(root, sum, res);
return res % M;
}
void dfs(TreeNode* node, long& sum) {
if (!node) return;
sum += node->val;
dfs(node->left, sum);
dfs(node->right, sum);
}
int helper(TreeNode* node, long sum, long& res) {
if (!node) return 0;
int cur = node->val + helper(node->left, sum, res) + helper(node->right, sum, res);
res = max(res, cur * (sum - cur));
return cur;
}
};
再来看一种更简洁的写法,这里并不需要一个单独的递归函数来计算整棵树的结点之和,而是可以利用上面的后序遍历的递归函数,因为其返回的就是以输入结点为根结点的子树的结点之和,而若输入的就是原来的根结点,则得到的就是整棵树的结点值和。但是由于此时输入的 sum 是0,所以得到的 res 结果也没有意义,需要再次调用递归函数,此时的 sum 就可以传入正确的值了,从而得到的 res 也是正确的,参见代码如下:
解法二:
class Solution {
public:
int maxProduct(TreeNode* root) {
long res = 0, sum = 0, M = 1e9 + 7;
sum = dfs(root, sum, res);
dfs(root, sum, res);
return res % M;
}
int dfs(TreeNode* node, long sum, long& res) {
if (!node) return 0;
int cur = node->val + dfs(node->left, sum, res) + dfs(node->right, sum, res);
res = max(res, cur * (sum - cur));
return cur;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1339
类似题目:
Count Nodes With the Highest Score
参考资料:
https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/
LeetCode All in One 题目讲解汇总(持续更新中…)
(欢迎加入博主的知识星球,博主将及时答疑解惑,并分享刷题经验与总结,快快加入吧~)
微信打赏
 |
|
Venmo 打赏

—|—
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com





