1302. Deepest Leaves Sum

置顶

Created At : 2023-10-28 15:14

Count:1.2k Views 👀 :

Given the root of a binary tree, return the sum of values of its deepest leaves.

Example 1:

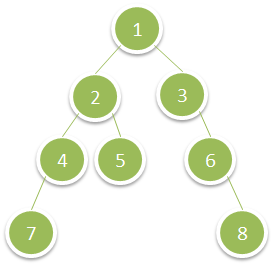
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

Example 2:

Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 19

Constraints:

The number of nodes in the tree is in the range [1, 104].
1 <= Node.val <= 100

这道题给了一棵二叉树，让返回最深的叶结点之和，难点主要是如何找到所有的最深叶结点，如果只是让把所有的叶结点加起来就会简单许多，但这里要求的是最深一层的叶结点。对于和二叉树的层相关的题，采用层序遍历是一种很好的选择，也就是一种 BFS 的遍历方法，要使用 queue 来辅助遍历了。对于每层都把叶结点值累加到 sum 中，然后在当前遍历完成了之后将其赋值给结果 res，这样最后一层遍历完了之后，最深的叶结点之和就找出来了。由于需要知道每一层的结束位置，这里在 while 循环中嵌套了一个 for 循环，为了防止 queue 的大小变化，采用的是初始化为 queue 的大小的方法。for 循环里面的写法就是一般的 BFS 的写法了，取出队列首元素，若是叶结点，则将其值累加到 sum 中，若其左右子结点存在，则加入队列中。for 循环结束后，将 sum 赋值给结果 res 即可，参见代码如下：

解法一：

class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        int res = 0;
        queue<TreeNode*> q{{root}};
        while (!q.empty()) {
            int sum = 0;
            for (int i = q.size(); i > 0; --i) {
                TreeNode *t = q.front(); q.pop();
                if (!t->left && !t->right) sum += t->val;
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            res = sum;
        }
        return res;
    }
};

二叉树的题目一般都可以用递归来解，这道题也不例外，虽然可能稍微麻烦了一些。由于 DFS 是深度优先遍历，所以可能会穿越不同的层，这里就需要一个变量 level 来表示当前层数，用 mxLevel 表示当前已经探明的最大层数。在递归函数中，首先判空，然后判断若 level 大于 mxLevel，说明当前到达更深一层了，则 mxLevel 更新为 level，并且重制结果 res 为0。若 level 等于 mxLevel，说明当前层是已知的最深层，可以将结点值累加到 res 中。然后分别对左右子结点调用递归函数，记得层数 level 要自增1，参见代码如下：

解法二：

class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        int res = 0, mxLevel = 0;
        dfs(root, 0, mxLevel, res);
        return res;
    }
    void dfs(TreeNode* node, int level, int& mxLevel, int& res) {
        if (!node) return;
        if (level > mxLevel) {
            mxLevel = level;
            res = 0;
        }
        if (level == mxLevel) {
            res += node->val;
        }
        dfs(node->left, level + 1, mxLevel, res);
        dfs(node->right, level + 1, mxLevel, res);
    }
};

我们也可以统计所有层的结点之和，最后只要返回最后一层的值即可，因为最后一层的结点一定都是叶结点，并且是最深的叶结点。这里用一个一维数组 sums，其中 sums[i] 就表示第i层的结点之和，这里 sums 数组的长度其实就是当前已探索的最大层数，相当于上一种解法中的 mxLevel 变量。在递归函数中，还是先判空，然后判断 level 是否等于 sums 的长度，因为 level 是从0开始的，若其等于 sums 的长度，表示当前层已经超过了之前探明的层数，需要扩大 sums 的长度，可以把当前结点值加入到 sums 中。若 level 小于 sums 的长度，说明当前层是之前就已经探明的，则将当前结点值加到 sums[level]。然后再分别对左右子结点调用递归函数，记得层数 level 要自增1，参见代码如下：

解法三：

class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        vector<int> sums;
        dfs(root, 0, sums);
        return sums.back();
    }
    void dfs(TreeNode* node, int level, vector<int>& sums) {
        if (!node) return;
        if (level == sums.size()) {
            sums.push_back(node->val);
        } else {
            sums[level] += node->val;
        }
        dfs(node->left, level + 1, sums);
        dfs(node->right, level + 1, sums);
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1302

参考资料：

https://leetcode.com/problems/deepest-leaves-sum/

https://leetcode.com/problems/deepest-leaves-sum/discuss/463239/JavaC%2B%2BPython-Level-Traversal

https://leetcode.com/problems/deepest-leaves-sum/discuss/565187/Java-Recursive-faster-than-100.00

https://leetcode.com/problems/deepest-leaves-sum/discuss/1152922/JS-Python-Java-C%2B%2B-or-Easy-BFS-or-Recursive-DFS-Solutions-w-Explanation

LeetCode All in One 题目讲解汇总(持续更新中…)

（欢迎加入博主的知识星球，博主将及时答疑解惑，并分享刷题经验与总结，快快加入吧～）

喜欢请点赞，疼爱请打赏❤️.