1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

置顶

Created At : 2023-10-28 15:14

Count:1.2k Views 👀 :

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

A binary matrix is a matrix with all cells equal to 0 or 1 only.

A zero matrix is a matrix with all cells equal to 0.

Example 1:

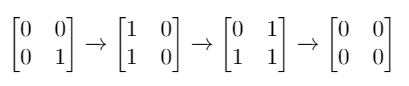
Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We do not need to change it.

Example 3:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix cannot be a zero matrix.

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 3
mat[i][j] is either 0 or 1.

这道题给了一个 m by n 的二维数组，只包含数字0或者1，现在说是可以任意选一个位置翻转数字，同时该位置周围的四个位置（若存在的话）也需要被反转，问最少需要翻转多少次可以将整个数组变为只含有0的数组。通过分析题目给的例子不难理解题意，首先来想，如果不考虑代码实现，给你一个任意数组，该怎么翻转成全0的数组，实际上是不好做的，因为很有可能翻转成之前已经存在的状态，并一直重复下去，很难翻成全0数组。这就像是一个迷宫，起始状态就是给定的数组，结束状态就是全0的数组，那么遍历迷宫的最少步数就是需要用广度优先遍历 Breadth-first Search 来做。每一个位置的状态就是当前数组的值，直接保留二维数组的话运算起来不是很高效，因为需要查重运算。这里用一个 trick 把二维数组编码成一个整型数，因为题目限定了m和n的大小不超过3，则数组中最多只有9个数字，可以把每个数字放到整型数的一个 bit 上，正好数组中只有0和1，可以完美的表示成二进制数，这样每个数组的情况就可以用一个二进制数表示了，理解了这个之后代码也就不难写了。

首先把起始状态编码成一个整型数，做法是把二维坐标变成一维坐标，通过 i*n + j 来实现，然后再将 mat[i][j] 左移 i*n + j 位，或 上 start 即可。然后就是 BFS 的传统写法了，用一个队列 queue，把 start 放进去，再用一个 HashSet 来查重，把 start 放进去。进行 while 循环，里面再用一个 for 循环，保证了是一层一层向外扩散的。先取出队首元素 cur，若 cur 为0，表示当前的数组全为0了，把当前步数 res 返回即可。否则就要尝试将每个数字都翻转一下，看是否会生成新的状态，遍历二维数组的每个位置，复制 cur 到 next，然后要翻转当前位置和相邻的四个位置，这样 dirs 数组中就有5个 offset 值，若新位置没有越界，则将 next 对应的 bit 位翻转，然后看这个新的整型数是否在 HashSet 中，不在的话加入 HashSet，并且排入队列继续遍历。每遍历完一层，步数 res 自增1，若 while 退出，返回 -1 即可，参见代码如下：

class Solution {
public:
    int minFlips(vector<vector<int>>& mat) {
        int res = 0, m = mat.size(), n = mat[0].size(), start = 0;
        vector<vector<int>> dirs{{0, 0}, {-1, 0}, {0, 1}, {1, 0}, {0, -1}};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                start |= mat[i][j] << (i * n + j);
            }
        }
        queue<int> q{{start}};
        unordered_set<int> visited{{start}};
        while (!q.empty()) {
            for (int t = q.size(); t > 0; --t) {
                int cur = q.front(); q.pop();
                if (cur == 0) return res;
                for (int i = 0; i < m; ++i) {
                    for (int j = 0; j < n; ++j) {
                        int next = cur;
                        for (auto dir : dirs) {
                            int x = i + dir[0], y = j + dir[1];
                            if (x < 0 || x >= m || y < 0 || y >= n) continue;
                            next ^= 1 << (x * n + y);
                        }
                        if (!visited.count(next)) {
                            visited.insert(next);
                            q.push(next);
                        }
                    }
                }
            }
            ++res;
        }
        return -1;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1284

类似题目：

Minimum Operations to Remove Adjacent Ones in Matrix

Remove All Ones With Row and Column Flips

Remove All Ones With Row and Column Flips II

参考资料：

https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/

https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/discuss/446342/JavaPython-3-Convert-matrix-to-int%3A-BFS-and-DFS-codes-w-explanation-comments-and-analysis.

LeetCode All in One 题目讲解汇总(持续更新中…)

喜欢请点赞，疼爱请打赏❤️.

微信打赏