Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.
Return the number of closed islands.
Example 1:
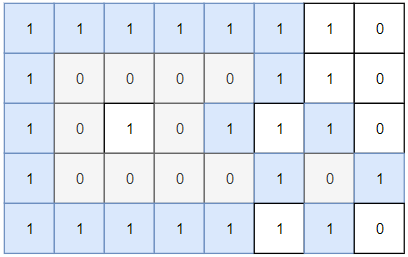
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation:
Islands in gray are closed because they are completely surrounded by water (group of 1s).
Example 2:
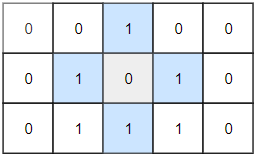
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1
Example 3:
Input: grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
Output: 2
Constraints:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
这道题给了一个只包含0和1的二维数组 grid,说是0代表陆地,1代表海洋,现在定义了被海洋上下左右包围的陆地为岛屿,现在问有多少个岛屿,注意岛屿必须被海洋完全包围,和边界相连的陆地不算是岛屿。既然岛屿是多个为0相连而形成的,那么肯定是要用 BFS 或 DFS 来找到连通区域的,难点是怎么确定找到的连通区域是不是一个岛屿,关键在于若某个连通区域和边界相连了,则其就不是岛屿了。我们可以反过来操作一下,首先把所有和边界相连的连通区域都找出来并标记,这样之后再找到的连通区域就一定是岛屿了。所以先遍历一遍数组,遇到边界上的陆地,则开始 DFS 遍历,并标记连通区域,完成了之后,再次遍历一遍数组,遇到边界上的陆地,则开始 DFS 遍历,并标记连通区域,此时找到一个连通区域之后就可以增加岛屿的个数了,参见代码如下:
解法一:
class Solution {
public:
int closedIsland(vector<vector<int>>& grid) {
int res = 0, m = grid.size(), n = grid[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if ((i == 0 || i == m - 1 || j == 0 || j == n - 1) && grid[i][j] == 0) {
dfs(grid, i, j);
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] != 0) continue;
dfs(grid, i, j);
++res;
}
}
return res;
}
void dfs(vector<vector<int>>& grid, int i, int j) {
int m = grid.size(), n = grid[0].size();
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] != 0) return;
grid[i][j] = 2;
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
};
我们也可以只遍历一次,在递归函数里做些改动从而区分是否为岛屿,此时让 dfs 函数具有返回值,返回0表示不是岛屿,返回1表示是岛屿。在递归函数中,若越界了,则返回0,表示直接跟边界相连了,肯定不是岛屿,否则若当前数值大于0了,表示要么遇到海洋了,要么是之前已经遍历过了,返回1。否则标记当前位置为2(标记成1也行,没太大影响),然后对四个邻居位置分别调用递归,并把四个结果乘起来,这里的乘法操作是精髓,因为只要其中有一个是0(遇到边界了),结果就是0了,表示不是岛屿。这里的相乘操作也可以替换为位运算的相’与’的操作 &,但注意一定不能用逻辑运算的’且’操作 &&,因为这个会短路后面的递归调用,从而可能导致连通区域无法被完全标记,参见代码如下:
解法二:
class Solution {
public:
int closedIsland(vector<vector<int>>& grid) {
int res = 0, m = grid.size(), n = grid[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) res += dfs(grid, i, j);
}
}
return res;
}
int dfs(vector<vector<int>>& grid, int i, int j) {
int m = grid.size(), n = grid[0].size();
if (i < 0 || i >= m || j < 0 || j >= n) return 0;
if (grid[i][j] > 0) return 1;
grid[i][j] = 2;
return dfs(grid, i + 1, j) * dfs(grid, i - 1, j) * dfs(grid, i, j + 1) * dfs(grid, i, j - 1);
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1254
参考资料:
https://leetcode.com/problems/number-of-closed-islands/
LeetCode All in One 题目讲解汇总(持续更新中…)
喜欢请点赞,疼爱请打赏❤️.
微信打赏
 |
|
Venmo 打赏

—|—
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




