In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0) and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).
In one move the snake can:
- Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
- Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
- Rotate clockwise if it’s in a horizontal position and the two cells under it are both empty. In that case the snake moves from
(r, c)and(r, c+1)to(r, c)and(r+1, c).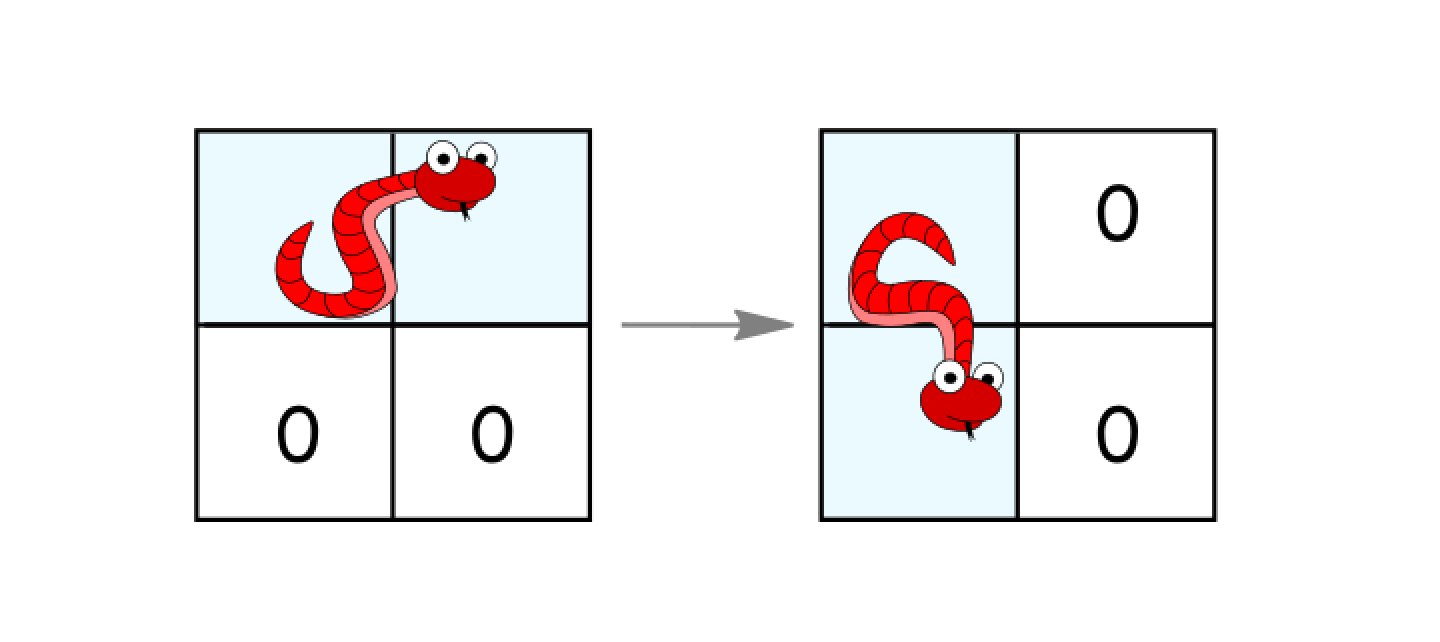
- Rotate counterclockwise if it’s in a vertical position and the two cells to its right are both empty. In that case the snake moves from
(r, c)and(r+1, c)to(r, c)and(r, c+1).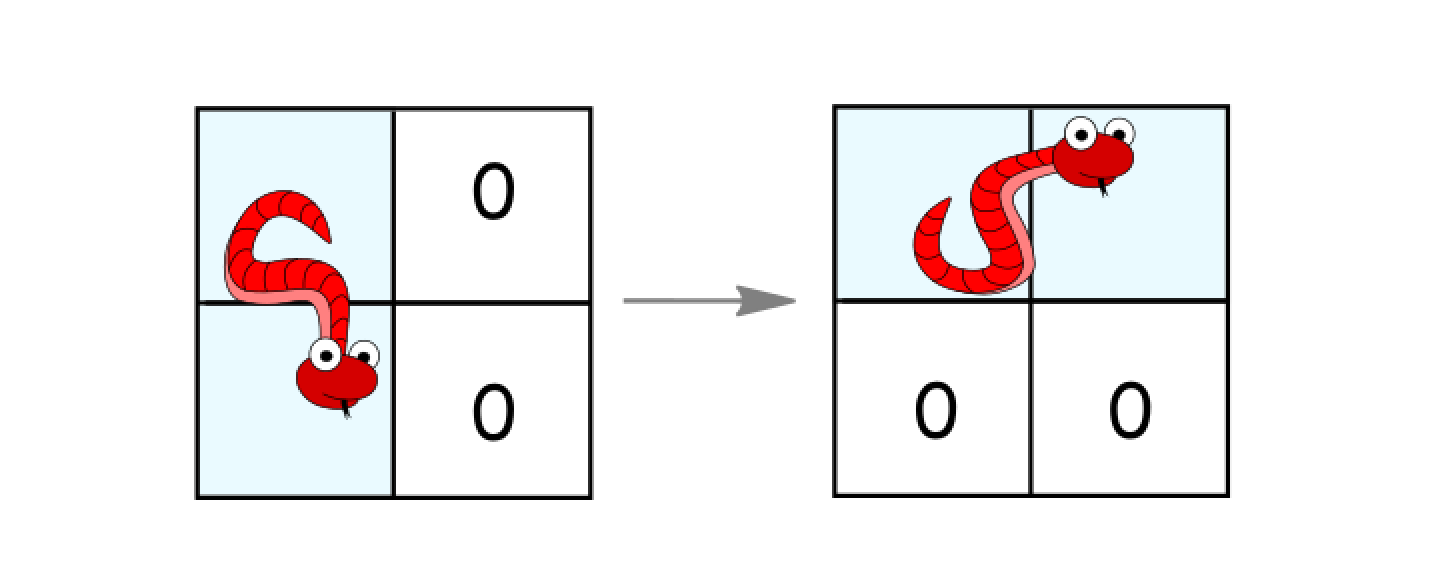
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return -1.
Example 1:
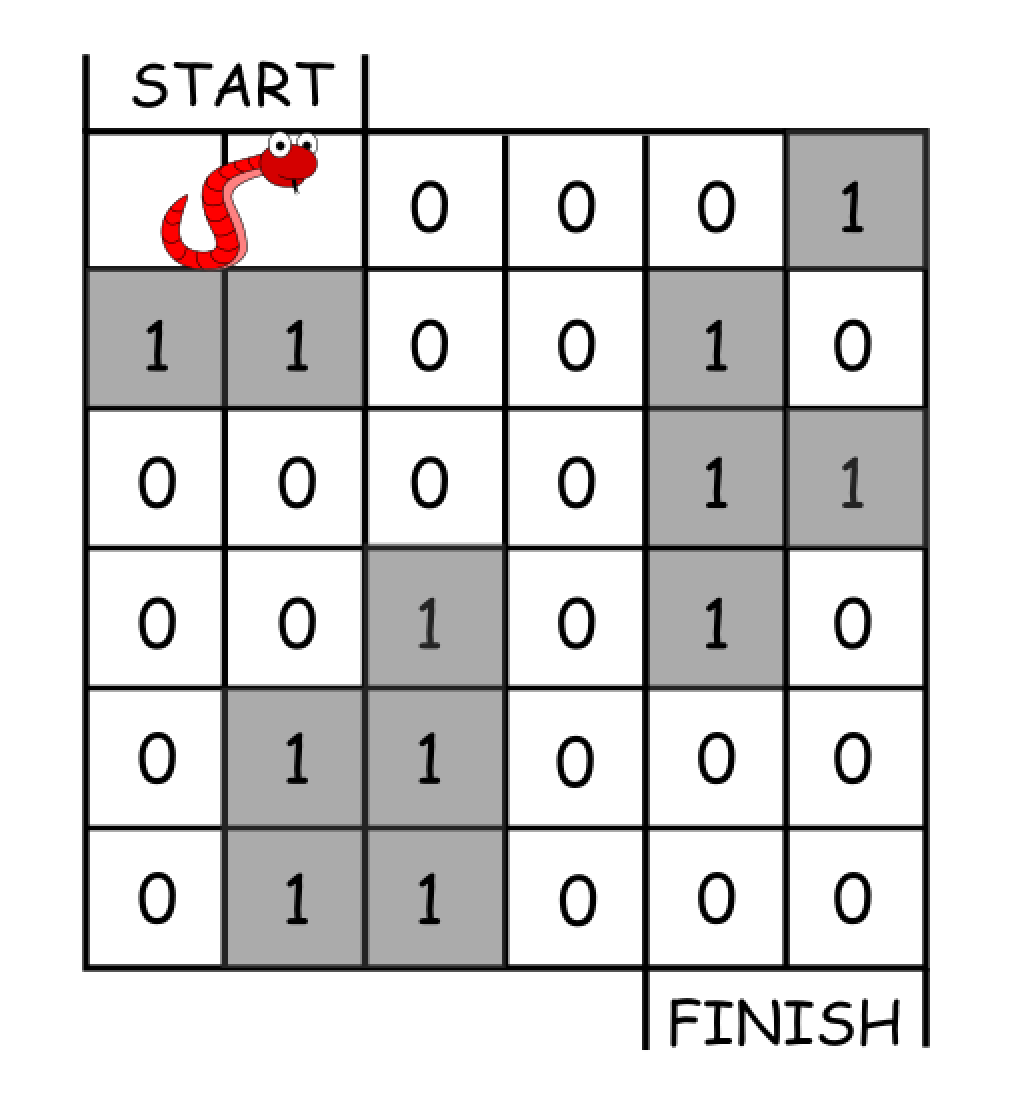
Input: grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
Output: 11
Explanation: One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].
Example 2:
Input: grid = [[0,0,1,1,1,1],
[0,0,0,0,1,1],
[1,1,0,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,1],
[1,1,1,0,0,0]]
Output: 9
Constraints:
2 <= n <= 1000 <= grid[i][j] <= 1- It is guaranteed that the snake starts at empty cells.
这道题给了个 n by n 的二维数组 grid,只有0和1两个数字,说是有个占两个位置 (0, 0) 和 (0, 1) 的蛇,问是否可以移动到 (n-1, n-2) 和 (n-1, n-1) 位置,能的话返回最少步数,不能的话返回 -1。注意蛇只能走数字0的地方,而且蛇只有竖直和水平两种姿势,只能有三种行动模式:第一种是向右移动,当蛇是水平姿势时,向右移动一格(前提是右边的格子为0),当蛇是竖直姿势时,蛇头蛇尾同时向右移动一格(前提是右边的两个格子为0)。第二种是向下移动,当蛇是水平姿势时,蛇头蛇尾同时向下移动一格(前提是下边的两个格子为0),当蛇是竖直姿势时,向下移动一格(前提是下边的格子为0)。第三种是旋转,分为顺时针旋转和逆时针旋转,当蛇是水平姿势时,顺时针旋转 90 度变为竖直姿势,蛇尾位置不变,当蛇是竖直姿势时,逆时针旋转 90 度变为水平姿势,蛇尾位置不变。语言干说有些苍白,好在题目中给了图示,还十分贴心地画出了一条萌萌的小红蛇,画风满分💯。其实这道题本质上还是一道迷宫遍历的题目,只不过不再是简单的上下左右四个方向移动,而是变成更为复杂的移动方式,不然怎么对得起其 Hard 的身价。但核心本质还是没变,既然是求最少步数,就是要用广度优先遍历 Breadth-first Search 来做。
先来想想,该如何表示蛇的某一个状态,首先蛇是占两个格子,分蛇头和蛇尾,其次,蛇还有水平和竖直两种姿势。这里蛇的姿势肯定要保存在状态里,用0表示水平,1表示竖直,还有就是蛇的位置也要记录,这里没必要同时记录两个位置,而是只用蛇头位置加上姿势,三个变量组成的状态即可。这里将初始状态 {0, 1, 0} 放入队列 queue 和 visited 集合中,其中 (0, 1) 是初始时蛇头的位置,0表示水平姿势。然后开始 BFS 的循环遍历,由于需要统计最小步数,所以中间用个 for 循环来一次遍历每一步可到达的所有位置。取出队首状态,若当前的蛇头位置已经到达了 (n-1 ,n-1),且姿势是水平,表示遍历已经完成了,返回当前步数 res 即可。否则分为水平和竖直两个姿势分别进行处理,若是水平姿势,则此时先判断蛇是否能右移,只需要判断右边的位置是否为0,且没有被访问过,可以到达的话将下个状态排入队列中。再来看是否能下移和旋转,这两个操作的共同的点是需要蛇下方的两个位置都是0,所以放一起判断,若下移和旋转后的状态未出现过,则排入队列中。对于竖直姿势,也是类似的操作,先判断蛇是否能下移,只需要判断下边的位置是否为0,且没有被访问过,可以到达的话将下个状态排入队列中。再来看是否能右移和旋转,这两个操作的共同的点是需要蛇右边的两个位置都是0,所以放一起判断,若右移和旋转后的状态未出现过,则排入队列中。最后别忘了步数 res 自增1,若 while 循环退出了,表示没法到达目标点,返回 -1 即可,参见代码如下:
解法一:
class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
int res = 0, n = grid.size();
set<vector<int>> visited{{0, 1, 0}};
queue<vector<int>> q;
q.push({0, 1, 0});
while (!q.empty()) {
for (int i = q.size(); i > 0; --i) {
auto t = q.front(); q.pop();
int x = t[0], y = t[1], dir = t[2];
if (x == n - 1 && y == n - 1 && dir == 0) return res;
if (dir == 0) { // horizontal
if (y + 1 < n && grid[x][y + 1] == 0 && !visited.count({x, y + 1, 0})) { // Move right
visited.insert({x, y + 1, 0});
q.push({x, y + 1, 0});
}
if (x + 1 < n && y > 0 && grid[x + 1][y - 1] == 0 && grid[x + 1][y] == 0) {
if (!visited.count({x + 1, y, 0})) { // Move down
visited.insert({x + 1, y, 0});
q.push({x + 1, y, 0});
}
if (!visited.count({x + 1, y - 1, 1})) { // Rote
visited.insert({x + 1, y - 1, 1});
q.push({x + 1, y - 1, 1});
}
}
} else { // vertical
if (x + 1 < n && grid[x + 1][y] == 0 && !visited.count({x + 1, y, 1})) { // Move down
visited.insert({x + 1, y, 1});
q.push({x + 1, y, 1});
}
if (y + 1 < n && x > 0 && grid[x - 1][y + 1] == 0 && grid[x][y + 1] == 0) {
if (!visited.count({x, y + 1, 1})) { // Move right
visited.insert({x, y + 1, 1});
q.push({x, y + 1, 1});
}
if (!visited.count({x - 1, y + 1, 0})) { // Rotate
visited.insert({x - 1, y + 1, 0});
q.push({x - 1, y + 1, 0});
}
}
}
}
++res;
}
return -1;
}
};
上面的方法虽然能过 OJ,但也是险过,来想想到底哪个地方比较耗时。对于一般的 BFS,大多情况下都是用 HashSet 来记录访问过的状态,由于这里的状态由三个变量组成,所以组成数组后放到 TreeSet 中了。一种优化方法就是将三个变量 encode 成一个字符串,这样就可以用 HashSet 了,查找就是常数级的复杂度了。还有一种方法就是直接利用 grid 数组来记录蛇的姿势,因为原来的 grid 数组只有0和1,只有一位,可以用第二位表示是否是竖直(通过’或’上2来改变状态),第三位表示是否是水平(通过’或’上4来改变状态)。队列中还是保存位置和姿势信息,但是这里稍微变一下,记录蛇尾的位置,因为蛇尾在旋转操作时不会改变,能稍微简单一些。在 while 循环中,还是用个内部 for 循环进行层序遍历,取出队首状态,若此时蛇尾已经到了 (n-1, n-2),直接返回步数 res 即可。那你可能会问,为啥此时不用判断蛇的姿势了呢?因为若此时蛇是竖直姿势的话,蛇头就越界了,这种非法状态根本不会排入队列中。结下来就是判断当前状态是否出现过了,由于蛇只能往右边和下边移动,所以很难走到之前的位置,唯一可能出现的重复状态是姿势,因为旋转的时候蛇尾位置不变,所以这里只要判读当前位置的姿势是否出现过。由于之前说了使用第二位和第三位来分别记录竖直和水平姿势,所以这里判断 dir,若是1(表示竖直),则’或’上数字2,若是0(表示水平),则’或’上数字4。取出对应位上的数字后判断,若是1,则表示当前状态已经处理过了,则跳过,否则就将对应位上的数字置为1。
接下来就要判断能否移动或旋转了,跟上面分姿势讨论不同的是,这里是直接判断是否能进行移动或旋转,而且分别放到一个子函数中,这样更加清晰一些。对于 canGoDown 函数,若蛇是水平姿势,判断下面两个位置的 grid 值是否越界,且最低位是否为0,因为第二三位可能不为0,所以不能直接判断 grid 值是否为0,而是要’与’上1取出最低位。若蛇是竖直姿势,判断下边一个位置是否越界,且最低位是否为0。对于 canGoRight 函数,若蛇是水平姿势,判断右边一个位置是否越界,且最低位是否为0。若蛇是竖直姿势,判断右边两个位置的 grid 值是否越界,且最低位是否为0。对于 canRotate 函数,不管蛇是水平还是竖直姿势,蛇尾的位置都不变,需要判断蛇尾的右边,下边,和右下边位置的 grid 值的最低位是否为0。若可以移动或者旋转,则将目标状态排入队列 queue 中。最后别忘了步数 res 自增1,若 while 循环退出了,表示没法到达目标点,返回 -1 即可,参见代码如下:
解法二:
class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
int res = 0, n = grid.size();
queue<vector<int>> q;
q.push({0, 0, 0}); // 0 is horizontal, 1 is vertial
while (!q.empty()) {
for (int i = q.size(); i > 0; --i) {
auto t = q.front(); q.pop();
int x = t[0], y = t[1], dir = t[2];
if (x == n - 1 && y == n - 2) return res;
if ((grid[x][y] & (dir ? 2 : 4)) != 0) continue;
grid[x][y] |= (dir ? 2 : 4);
if (canGoDown(grid, x, y, dir)) q.push({x + 1, y, dir});
if (canGoRight(grid, x, y, dir)) q.push({x, y + 1, dir});
if (canRotate(grid, x, y)) q.push({x, y, !dir});
}
++res;
}
return -1;
}
bool canGoDown(vector<vector<int>>& grid, int x, int y, int dir) {
int n = grid.size();
if (dir == 0) return x + 1 < n && (grid[x + 1][y] & 1) == 0 && (grid[x + 1][y + 1] & 1) == 0;
return x + 2 < n && (grid[x + 2][y] & 1) == 0;
}
bool canGoRight(vector<vector<int>>& grid, int x, int y, int dir) {
int n = grid.size();
if (dir == 0) return y + 2 < n && (grid[x][y + 2] & 1) == 0;
return y + 1 < n && (grid[x][y + 1] & 1) == 0 && (grid[x + 1][y + 1] & 1) == 0;
}
bool canRotate(vector<vector<int>>& grid, int x, int y) {
int n = grid.size();
return x + 1 < n && y + 1 < n && (grid[x + 1][y] & 1) == 0 && (grid[x][y + 1] & 1) == 0 && (grid[x + 1][y + 1] & 1) == 0;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1210
参考资料:
https://leetcode.com/problems/minimum-moves-to-reach-target-with-rotations/
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




