There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
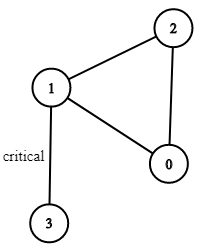
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.
Example 2:
Input: n = 2, connections = [[0,1]]
Output: [[0,1]]
Constraints:
2 <= n <= 10^5n - 1 <= connections.length <= 10^50 <= ai, bi <= n - 1ai != bi- There are no repeated connections.
这道题说是有n个服务器互相连接,定义了一种关键连接,就是当去掉后,会有一部分服务无法访问另一些服务。说白了,就是让求无向图中的桥,对于求无向图中的割点或者桥的问题,需要使用塔里安算法 Tarjan’s Algorithm。该算法是图论中非常常用的算法之一,能解决强连通分量,双连通分量,割点和桥,求最近公共祖先(LCA)等问题,可以参见知乎上的这个贴子。Tarjan 算法是一种深度优先遍历 Depth-first Search 的算法,而且还带有一点联合查找 Union Find 的影子在里面。和一般的 DFS 遍历不同的是,这里用了一个类似时间戳的概念,就是用一个 time 数组来记录遍历到当前结点的时间,初始化为1,每遍历到一个新的结点,时间值就增加1。这里还用了另一个数组 low,来记录在能够访问到的所有节点中,时间戳最小的值,这样,在一个环上的结点最终 low 值都会被更新成一个最小值,就好像 Union Find 中同一个群组中都有相同的 root 值一样。这是非常重要且聪明的处理方式,因为若当前结点是割点的话,即其实桥一头的端点,当过桥之后,由于不存在其他的路径相连通(假设整个图只有一个桥),那么无法再回溯回来的,所以不管桥另一头的端点 next 的 low 值如何更新,其一定还是会大于 cur 的 low 值的,则桥就找到了。可能干讲不好理解,建议看下上面提到的知乎帖子,里面有图和视频可以很好的帮助理解。
这里首先根据给定的边来建立图的结构,这里使用 HashMap 来建立结点和其所有相连的结点集合之间的映射。对于每条边,由于是无向图,则两个方向都要建立映射,然后就调用递归,要传的参数还真不少,图结构,当前结点,前一个结点,cnt 值,time 和 low 数组,还有结果 res。在递归函数中,首先给当前结点 cur 的 time 和 low 值都赋值为 cnt,然后 cnt 自增1。接下来遍历和当前结点所有相邻的结点,若 next 的时间戳为0,表示这个结点没有被遍历过,则对该结点调用递归,然后用 next 结点的 low 值来更新当前结点的 low 值。若 next 结点已经之前访问过了,但不是前一个结点,则用 next 的 time 值来更新当前结点的 low 值。若回溯回来之后,next 的 low 值仍然大于 cur 的 time 值,说明这两个结点之间没有其他的通路,则一定是个桥,加入到结果 res 中即可,参见代码如下:
class Solution {
public:
vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
int cnt = 1;
vector<vector<int>> res;
vector<int> time(n), low(n);
unordered_map<int, vector<int>> g;
for (auto conn : connections) {
g[conn[0]].push_back(conn[1]);
g[conn[1]].push_back(conn[0]);
}
helper(g, 0, -1, cnt, time, low, res);
return res;
}
void helper(unordered_map<int, vector<int>>& g, int cur, int pre, int& cnt, vector<int>& time, vector<int>& low, vector<vector<int>>& res) {
time[cur] = low[cur] = cnt++;
for (int next : g[cur]) {
if (time[next] == 0) {
helper(g, next, cur, cnt, time, low, res);
low[cur] = min(low[cur], low[next]);
} else if (next != pre) {
low[cur] = min(low[cur], time[next]);
}
if (low[next] > time[cur]) {
res.push_back({cur, next});
}
}
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1192
参考资料:
https://leetcode.com/problems/critical-connections-in-a-network/
https://zhuanlan.zhihu.com/p/101923309
LeetCode All in One 题目讲解汇总(持续更新中…)
转载请注明来源于 Grandyang 的博客 (grandyang.com),欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 grandyang@qq.com




