119. Pascal's Triangle II

置顶

Created At : 2023-10-28 15:14

Count:822 Views 👀 :

Given a non-negative index k where k ≤ 33, return the k th index row of the Pascal’s triangle.

Note that the row index starts from 0.

In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O ( k ) extra space?

杨辉三角想必大家并不陌生，应该最早出现在初高中的数学中，其实就是二项式系数的一种写法。

　　　　　　　　１
　　　　　　　１　１
　　　　　　１　２　１
　　　　　１　３　３　１
　　　　１　４　６　４　１
　　　１　５　10　10　５　１
　　１　６　15　20　15　６　１
　１　７　21　35　35　21　７　１
１　８　28　56　70　56　28　８　１

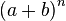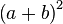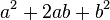杨辉三角形第n层（顶层称第0层，第1行，第n层即第 n+1 行，此处n为包含0在内的自然数）正好对应于二项式 $\\left$a+b\\right$^{n}$ 展开的系数。例如第二层 1 2 1 是幂指数为2的二项式 $\\left$a+b\\right$^{2}$ 展开形式 $a^{2}+2ab+b^{2}$ 的系数。

杨辉三角主要有下列五条性质：

杨辉三角以正整数构成，数字左右对称，每行由1开始逐渐变大，然后变小，回到1。
第 $n$ 行的数字个数为 $n$ 个。
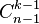第 $n$ 行的第 $k$ 个数字为组合数 $C_{n-1}^{k-1}$ 。
第 $n$ 行数字和为 $2^{n-1}$ 。
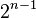除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和（也就是说，第 $n$ 行第 $k$ 个数字等于第 $n-1$ 行的第 $k-1$ 个数字与第 $k$ 个数字的和）。这是因为有组合恒等式： $C_{n}^{i}=C_{n-1}^{i-1}+C_{n-1}^{i}$ 。可用此性质写出整个杨辉三角形。

由于题目有额外限制条件，程序只能使用 O(k) 的额外空间，那么这样就不能把每行都算出来，而是要用其他的方法, 我最先考虑用的是第三条性质，算出每个组合数来生成第n行系数，代码请参见评论区一楼。本地调试输出前十行，没啥问题，拿到 OJ 上测试，程序在第 18 行跪了，中间有个系数不正确。那么问题出在哪了呢，仔细找找，原来出在计算组合数那里，由于算组合数时需要算连乘，而整型数 int 的数值范围只有 -32768 到 32768 之间，那么一旦n值过大，连乘肯定无法计算。而丧心病狂的 OJ 肯定会测试到成百上千行，所以这个方法不行。那么我们再来考虑利用第五条性质，除了第一个和最后一个数字之外，其他的数字都是上一行左右两个值之和。那么我们只需要两个 for 循环，除了第一个数为1之外，后面的数都是上一次循环的数值加上它前面位置的数值之和，不停地更新每一个位置的值，便可以得到第n行的数字，具体实现代码如下：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1);
        res[0] = 1;
        for (int i = 1; i <= rowIndex; ++i) {
            for (int j = i; j >= 1; --j) {
                res[j] += res[j - 1];
            }
        }
        return res;
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/119

类似题目：

Pascal’s Triangle

参考资料：

https://leetcode.com/problems/pascals-triangle-ii/

https://leetcode.com/problems/pascals-triangle-ii/discuss/38420/Here-is-my-brief-O(k)-solution

https://leetcode.com/problems/pascals-triangle-ii/discuss/38478/My-accepted-java-solution-any-better-code

LeetCode All in One 题目讲解汇总(持续更新中…)

转载请注明来源于 Grandyang 的博客 (grandyang.com)，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 grandyang@qq.com