1105. Filling Bookcase Shelves

置顶

Created At : 2023-10-28 15:14

Count:788 Views 👀 :

We have a sequence of books: the i-th book has thickness books[i][0] and height books[i][1].

We want to place these books in order onto bookcase shelves that have total width shelf_width.

We choose some of the books to place on this shelf (such that the sum of their thickness is <= shelf_width), then build another level of shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.

Note again that at each step of the above process, the order of the books we place is the same order as the given sequence of books. For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

Example 1:

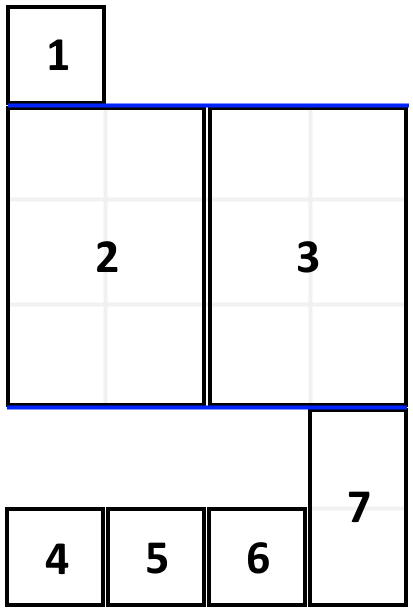
Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelf_width = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves are 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

Constraints:

1 <= books.length <= 1000
1 <= books[i][0] <= shelf_width <= 1000
1 <= books[i][1] <= 1000

这道题说是让用书来填书架，每本书有其固定的宽和高，需要按给定的顺序来排列书，要么排在新的一行，要么排在之前的层，注意每层的宽度不能超过给定的 shelf_width 的限制，每层的高度按照最高的那本书来计算，问怎么安排才能使得整个书架的高度最小。这种数组玩极值的题目，大概率就是贪婪算法或者动态规划 Dynamic Programming，但是这里贪婪算法就不太合适，因为书的高度是不确定的，就算尽量每行尽可能的多放书，并不能保证整体的高度是最小的。所以只能祭出动态规划了，先来定义 DP 数组，这里使用一个一维的 dp 数组，其中 dp[i] 表示前i本书可以组成的最小高度，大小初始化为 n+1。接下来找动态转移方程，对于每一本新的书，最差的结果就是放到新的一行中，这样整个高度就增加了当前书的高度，所以 dp[i] 可以先赋值为 dp[i-1] + height，然后再进行优化。方法是不停加上之前的书，条件是总宽度不能超过给定值，高度选其中最高的一个，每次用 dp[j] + height 来更新 dp[i]，最终返回 dp[n] 即可，参见代码如下：

class Solution {
public:
    int minHeightShelves(vector<vector<int>>& books, int shelf_width) {
        int n = books.size();
        vector<int> dp(n + 1);
        for (int i = 1; i <= n; ++i) {
            int width = books[i - 1][0], height = books[i - 1][1];
            dp[i] = dp[i - 1] + height;
            for (int j = i - 2; j >= 0 && width + books[j][0] <= shelf_width; --j) {
                height = max(height, books[j][1]);
                width += books[j][0];
                dp[i] = min(dp[i], dp[j] + height);
            }            
        }
        return dp[n];
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1105

参考资料：

https://leetcode.com/problems/filling-bookcase-shelves/

https://leetcode.com/problems/filling-bookcase-shelves/discuss/323315/Java-DP-solution

https://leetcode.com/problems/filling-bookcase-shelves/discuss/323305/C%2B%2B-4-lines-DFS-%2B-Memo

LeetCode All in One 题目讲解汇总(持续更新中…)

转载请注明来源于 Grandyang 的博客 (grandyang.com)，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 grandyang@qq.com